Ripley's K function

Ripley's K function for the data is compared with the expected line y=x under Poisson distribution of the points (actually, a scaled version of K is used, called L: L is the square root of the quotient of K and pi). In addition, simulated Poisson fields of the same N for the same size study area are generated, as are corresponding Ripley's K functions; these give some idea of how extreme the result of the data's Ripley's K function is.

• We begin with a plot of the data:
  

  When I look at this pattern does not look significantly different from a Poisson pattern; when someone with a little more experience (like Dr. Art Getis) looks at it, they find that the pattern appears roughly evenly spaced in a roughly homogeneous plane (i.e. more regular than a Poisson process would produce).

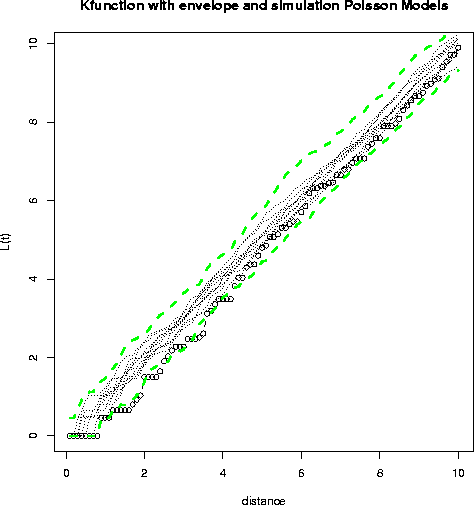
• This first plot is produced in R; the envelope shown is for 100 Poisson simulations (only 10 simulations are actually shown).
  

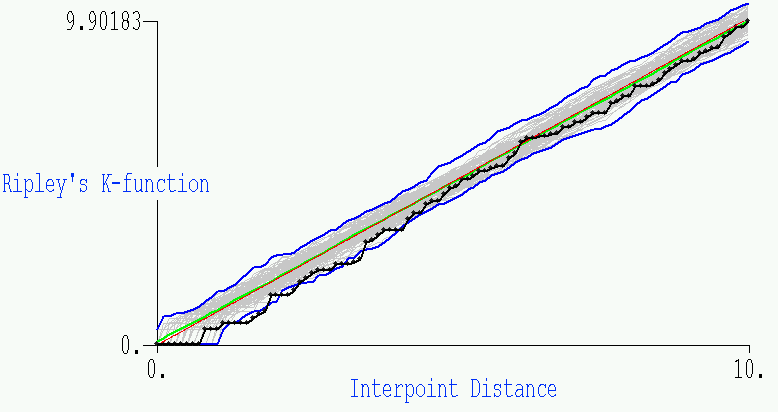
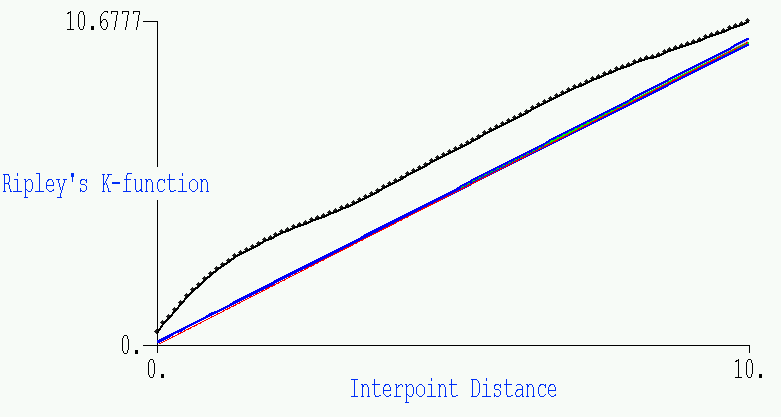
• This second plot is the related GeoMed output, where we show the same information (although the blue envelope is for the 10 simulations shown). The actual results from the data are given by the black function, with the points added on to show the 100 subintervals for which the function is plotted. The green and red in the center represent the average simulation and the function f(x)=x, respectively.
  

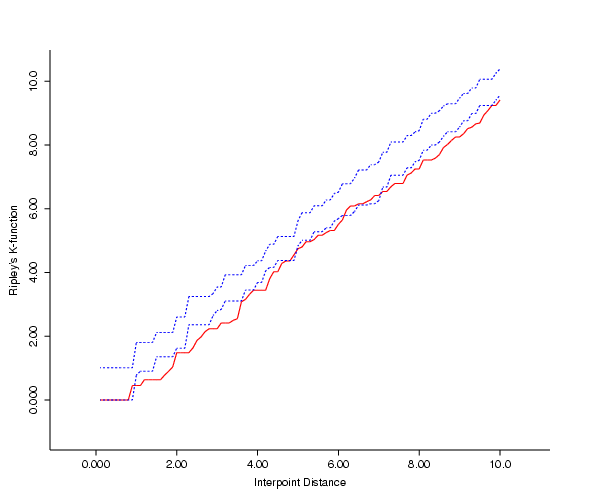
• The third plot was created in Xlispstat using the output of the web version of Dr. Getis's PPA software. PPA doesn't allow any adjustment of the region, but uses the minimum bounding rectangle (i.e., uses as rectangular boundaries the max and min x, y points). This was a convenience for the programmers, and Dr. Getis notes that one should use the actual study boundaries. In R one of the inputs is the bounding rectangular region for the point data; I've included this option in the GeoMed software.
  

• What conclusion might we draw? The fact that the K function of the data seems low by comparison with the Poisson simulated plots for small values of h might be interpreted as follows: towns are not likely to be located too close to each other, for, as Dr. Getis says, "the competitive economies of towns, especially in agricultural areas, requires that they be dispersed rather than random or clustered."

• Again, we begin with a plot of the data:
  

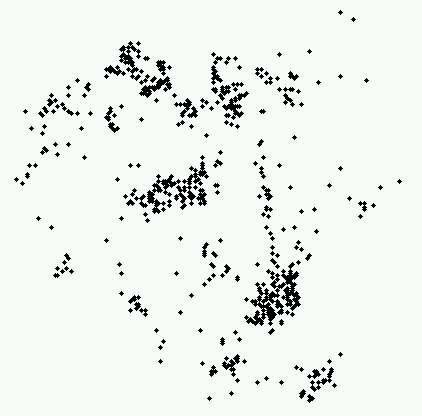
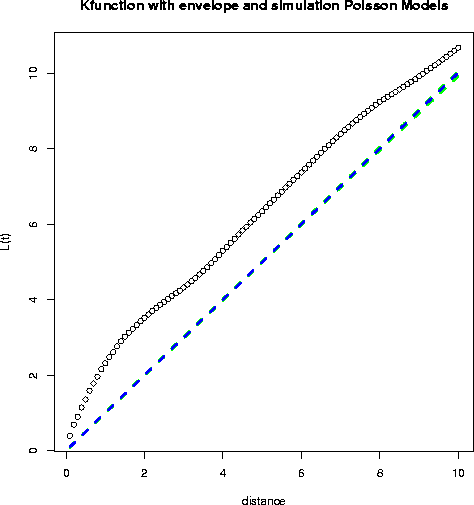
  As you can see, this pattern is significantly different from a Poisson pattern, with a very high intensity of cases close together.

• 

• 

• What conclusion might we draw? Obviously the Diggle data is significantly non-Poisson; the data cluster much more than expected under Complete Spatial Randomness, at least for scales below 10.

  Dr. Getis makes the following observation: "the distance at which the L(t) observation is above the random expectation (the dashed line) defines the extent of the clustering. In this case, I roughly make it out to be at a distance of 2. When the slope of the observed function becomes less than the random expectation, there is no longer a tendency for clustering. Notice that the clusters are about 2 in diameter."

Dr. Getis, of San Diego State University's Department of Geography and an expert and author in the field of spatial statistics, suggests that another comparison plot that is of interest is the comparison of two plots, e.g., a disease distribution and a susceptibles distribution.