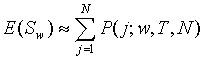
A test for temporal clustering in a single time series.

Data Requirements

Time series of case counts

time series must be at least five time cells in length

Window width

the test is most sensitive to clustering when the scanning window is the same width as natural clusters in the data

Analysis

H₀: Cases occur at random across the time series

H_a: Cases cluster in some time periods

Test Statistic: The maximum number of cases appearing in a pre-defined window as it is moved continuously along a time series. When the cases are clustered the maximum number of cases in the scanning window will be large. The expectation under the null hypothesis, E(S_w) is: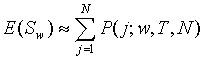

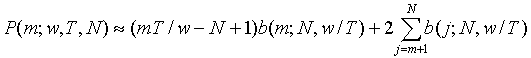
with

and where N is the total number of cases, T is the number of time periods, w is window width, and S_w is the maximum number of cases observed in w as it is slid along the time series. S_w is larger than its expectation when cases cluster in a few time cells. S_w is smaller than its expectation when cases are uniformly distributed among the time cells. The probability of observing, under the null hypothesis, an S_w given the window width w, T time periods and N cases is approximated by:

Here

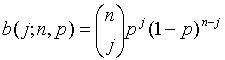
is a binomial coefficient. P(j;w, T, N) is the probability of obtaining, under the null hypothesis, a scan statistic greater than or equal to j. This probability is one-tailed.

Output

Total number of cases and the window width

The scan statistic, its expectation, and the p-value

Graph of S_w on its expectation with 45 degree line through origin

Reference

Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.