Lawson and Waller's Score test: Analysis

H_o: Observed number of cases in each region under study are independent, Poisson random variables with a common rate of disease

H_a: Observed number of cases in each region under study are independent, Poisson random variables where the rate of disease is an proportionally increasing function of exposure

Test statistic: Let g_i be the exposure to the focus for an individual residing in region i. Let O_i and E_i represent the observed and expected disease counts, under the null hypotheses, for regions i = 1,...,I. ( maximum exposure weight (g_I) assigned by GeoMed software = 1.0x10¹⁰ )

Expectation of the test statistic is zero under the null hypothesis and the variance is approximated by the following equation when baseline risk is known and provided by the user as an expected disease risk:

  and by the following equation when baseline risk is not known, and estimated from the sample population as an average risk:

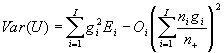
Where n_i is the population in region i, and n₊ is the total population size.

U has an asymptotic standard normal distribution for most cases except for very rare diseases:

from which a p-value can be calculated