There is a fascinating method for approximating areas of objects, based on randomness. It's curious and interesting that randomness (which we think of as related to nonsense) can be used to give us good approximations, but it's so.
The method is especially useful with irregular objects, for which formulas don't exist. For the arborloo exercise, let's compare the area of the ring and the loo in the following picture:
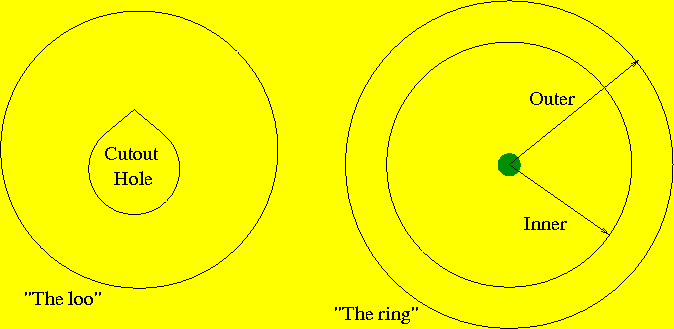
- Print off the picture.
- Fold the edges of the picture up to create a small rectangular box (ideally just slightly larger than the picture itself). Your picture needs to be flat for this to work well: if there are lots of bumps and ridges, your results will likely be poor.
- Measure the length and width of the box in inches, and calculate the area (since it's a rectangular box, the area is just the length times the width, in square inches).
- Count out 200 rice grains, and put them into the box.
- Now the next set of steps we're going to do over and over again, as long
as you have the patience and time. You'll create a table with two
columns, and as many rows as you can manage (like
this):
- shake the box well, then set it down (the grains of rice should be scattered all over the bottom)
- count the rice grains on the loo (don't count those in the poop hole!). Count all grains that are at least half on the loo.
- count the rice grains on the ring. Count all grains that are at least half on the loo.
- When you've run out of patience or time, you'll need to calculate the average number of grains on the loo and on the ring. To do that, you add up all the rice grains on each, and then divide by the number of times you counted. See the sample table (it has boxes for these calculations).
- Now: if both objects were the same area,
- How would the two averages be related?
- Because of the method we used, would you expect to see exactly that relationship?
- If not, how much inexactness would you be able to tolerate, and still believe that the areas were really the same?
- For further study:
- Because we don't expect to get exactly equal averages, the important question is "what's equal enough?" To decide that, we study the distributions of the two sets of data (for the loo, and for the ring). One test of equality: if the two objects both have the same area, then about half the time one object would have more rice grains, and about half the other time the other object would have more. 50% of the time each would be ahead of the other. To test this using your data, follow these steps.
- This method of calculating area is very useful and important. Its name is "Monte Carlo Integration", after the gambling center of Monte Carlo (because of the randomness and the use of probability).
Of course another way to do it is to actually throw darts! Cut out the picture, affix it to a dart board, and throw for the board (but don't try to hit any particular part). After you've thrown a few hundred darts, take off the picture, and compute the ratios for dots inside the loo (but not in the poop hole, as usual). You can compute the area of the rectangle: then, in a perfect world,