In Dan Griffith's module, a variety of techniques are applied to some example data.
We will use the Snow data to calculate a Moran's I, then use that
statistic to estimate the SAR (simultaneous autoregressive) autocorrelation
parameter ![]() , from
which we can calculate the effective sample size of the n=35 region data
set.
, from
which we can calculate the effective sample size of the n=35 region data
set.
Along the way is a review of some ArcView techniques, as well as a visit to Gamma (with a few little twists thrown in).
The objectives of this lab are as follows: you should
- Create new numerical variables within ArcView;
- Use MapStat from within ArcView to analyze a single geographic distribution of disease rates (Snow's data). In particular you will examine the effect of normalizing data on spatial autocorrelation;
- Use Gamma to analyze the Snow data, looking for spatial autocorrelation.
Lab
UMich students: pair up, if you'd like; always better to have a partner, in my opinion.
Exercise 1:
- Prior to firing up ArcView, you must install the MapStat extension.
Make sure you pick up the most current version, from the MapStat section of the
digitizing lab.
- Load the Snow files into ArcView.
This data was digitized from the BW image used in the Scientific
Visualization module. [If you want a few more details about this process,
view this page.]
- We'll begin by creating three new variables:
- the first is a rate (deaths per thousand of population),
- the second is a transformation of the rate variable, and
- the third is a BW -- binary -- variable created from the rates.
It's relatively easy to create a new variable from a given numerical variable in ArcView. The first two are the easiest, so we'll start with those.
- Open the attribute table of the theme to which the variable is to be added.
- From the Table menu choose "Start Editing".
- From the Edit menu, "Add Field" - it will ask you for some "Field Definitions". Give your field a meaningful name (use "rate" for the first one), choose the type, assign a width, and, if your field is numeric, choose the number of decimal places you want to keep. OK!
- From the Field menu, choose "Calculate". Select the variables and mathematical operations necessary to create the rate.
For the second variable (call it "trans") you saw in lecture that it is often the case that a variable which is not normally distributed will be transformed by a power (or log) transformation to create a new variable which is more normally distributed.
If you examine the histogram of the rate or quantile plot of the rate. The histogram of a normal variable should be bell-shaped; and the quantile-plot of a normal variable should be roughly a straight line. You notice that this variable does not appear to be normally distributed. We will now create a transformed variable from the original rate which is more normal in appearance. Many software packages contain routines to calculate the parameters of this optimal transformation: we're not interested in doing that here, and will simply transform according to the relation
trans = (rate - 1.45)^0.3 Type this equation into the Calculator to define the trans variable. Don't forget the 0 on 0.3; ArcView is so ignorant that it can't recognize .3 as 0.3.
In order to create the binary BW variable, use the criterion that BW=1 if bwval is greater than 5.5, and BW=0 if bwval is less than 5.5 (this creates a nearly perfect match with the Black/White plots from reading). Here's how:
- Make the View Window active.
- Query (the hammer icon
 ) those values of rate
>= 5.5; these ids will be selected. Click "New Set"
) those values of rate
>= 5.5; these ids will be selected. Click "New Set"
- Go back to the calculater and create the new field "bw" as 1 (this will only apply to the selected variable rows!).
- From the table menu, "Switch the selection":

- Calculate the variable bw as 0 (again, this will only apply to the selected rows).
- From the Table menu, "Stop Editing".
The transformed variable (trans) is reputedly (more) normal. We can verify this from the histogram of trans and from the quantile plots of trans. How have we done?
- We'll begin by creating three new variables:
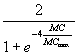 -
- 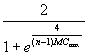 ,
,