Clearly, there are many measures of dissimilarity, distance and similarity. Which measure is appropriate in a given situation depends on the data and the nature of the scientific hypotheses being explored. To support maximum flexibility the Gamma software provides an equation editor for specifying distance, dissimilarity, and similarity measures. Once entered a measure may be used in other studies, and Gamma supports an expandable equation library for your convenience.

The equation editor is a powerful tool that parses, interprets and executes equations provided in the form of ASCII (text) strings. These strings (equations) may be entered directly into the distance metric dialog box, or they may be imported from an ASCII file. Equations are parsed when you press `Enter' after typing in the equation in the dialog box, or when they are loaded from an ASCII file. Any errors in the equation (such as a missing parenthesis) are reported during parsing. Prior to evaluating the Gamma product, the software calculates the distance matrix D by evaluating the distance metric equation for all pair-wise combinations of the locations.

To understand the equation editor consider how it represents spatial data. Assume we have observations on `zcount' variables at two locations, denoted 1 and 2. We represent the vector of observations at location 1 as V1 and the vector of observations at location 2 as V2. For example, suppose we measure concentrations of Cadmium and Lead at two sites. The concentrations are [Cd]=12ppm, [Pb]=0.2ppm at site 1 and [Cd]=42ppm, [Pb]=4.1ppm at site 2. The vectors are then V1={12, 0.2} and V2={42,4.1}. The character sequence `V1' uniquely identifies the vector of observations at site 1, and for simplicity we now drop the bold typing used to indicate vector quantities.

The equation editor allows you to reference specific variables using indexing of the form V1(i), where i is the index of the desired variable. For example, V1(1) is 12, and is the Cadmium concentration at site 1. The editor represents Gamma's spatial data sets as x, y, z1, z2, ..., zcount. The spatial coordinates (x, y) are not counted in this indexing system. Thus, if you observe only one variable (say case/control identity), case/control identity is referenced as variable 1.

Access to statistics calculated across all locations in the entire data set are provided by the special functions ZMax, ZMin, ZMean, ZMode, ZSum, ZStd and ZVar. For example, suppose we observe Cadmium and Lead concentrations at 5 sites. The maximum lead concentration out of all 5 sites is ZMax(2). Here `2' refers to the second variable (column) in the data set, which is Lead.

Gamma's equation editor supports the mathematical operations and functions in table 4-4. The precedence of operators is the same as that used by the C programming language. First, the contents of parentheses are evaluated, then multiplication and division (*, /) and then addition and subtraction (+, -). Functions are evaluated after the contents of their corresponding parenthetical argument.

For example, the expression is entered in the equation editor as sum(i,1,zcount,abs(V1(i)-V2(i))). The equation editor supports up to 6 levels of nested summations, and `sum2' is used to prevent inclusion of sums for which the indices have the same value. Thus the expression

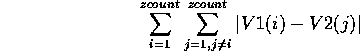
would be entered as sum(i,1,zcount,sum2(j,1,zcount,abs(V1(i)-V2(j)))). Exercises illustrating use of the equation editor are given in the next section.

Summary: Calculate the Manhattan distances for the data set Chapter_3.pnt. The data are the locations and dates (years) of five fires in a Northern Quebec hardwood forest from 1920 to 1983.

Data Set: Chapter_3.pnt is the first five records from file Fire.pnt; x and y are from a Universal Transverse Mercator projection and are kilometers east and north of an artificial origin; z is the year in which the fire occurred:

Protocol: Launch the Gamma software and initiate a new session.

1. Matrix File Format dialog: Set `Z File Coordinate Type' to `User Defined Coordinates'.

2. Quantify Distance Matrix dialog: Set `Choose a Z file' to Chapter_3.pnt, and `Distance Metric' to `Manhattan'. This will calculate the distance as . The data set has only one variable (time of fire occurrence) and this simplifies to , which is the waiting time between fires i and j.

3. Proximity Metric dialog: Set `proximity metric' to `Distance, point-point'. This will calculate the geographic distance between fires.

4. Step through the remaining screens in Gamma's wizard and press `Finish' on the `Monte Carlo' dialog. Then select `Matrices' on the menu bar, `Write matrices to an ASCII file' and `Distance'. This will write the distance matrix to the file `Chapter_3.dmx'. Use Notepad or another ASCII editor to view the distance matrix. It will contain several records of header information and the distance matrix:

The rows and columns correspond to the rows of the input data set. For example, the underlined element is d₂₁ and is the waiting time between fires at site 1 and site 2. Manhattan distances are in the range 0 to infinity, and take on values of 0 or 1 in this example because fires occur only in 1920 or 1921.

Problem: Repeat the above exercise but use the equation editor instead of the `radio button' for calculating Manhattan distances. You will need to follow all of the above steps, but in item `2. Quantify Distance Matrix dialog', click on `Custom' and type in the following equation:

sum(i,1,zcount,abs(z1(i)-z2(i)))

Then complete the exercise and above and inspect the file of distances. Are the distances the same? Now repeat this exercise but use this equation:

abs(z1(1)-z2(1))

Are the resulting distances the same? Which equation string is more general in terms of its applicability to data sets with different numbers of variables?

Summary: Geographic studies of disease outcomes often code cases as `1' and controls as `0'. A natural question is whether the spatial distribution of the cases is different from the spatial distribution of the controls. A significant aggregation of cases relative to the controls may indicate a disease cluster caused by contagion or exposure to a geographically localized risk factor. A convenient distance measure has the properties:

if and are both 1; 0 otherwise.

Thus the distance is 1 only when both i and j are cases, otherwise it is 0.

Problem: Define a distance measure that has the above properties and enter it into Gamma using the equation editor. Then apply it to the data set breastca.pnt (with user-defined coordinates) and export the distance matrix. Verify several of the distances by hand calculation to make sure they are correct. These data describe breast cancer in a neighborhood in Long Island, New York, and only one outcome (whether or not the woman has breast cancer) is recorded. Often, observations on several binary outcomes will be available. Would your distance measure work for multivariate binary data? Why or why not?