Name:

Directions: Show your work! Answers without justification will likely result in few points. Your written work also allows me the option of giving you partial credit in the event of an incorrect final answer (but good reasoning). Indicate clearly your answer to each problem (e.g., put a box around it). Good luck!

Problem 1 (25 pts). Calculate the following integrals using an appropriate integration technique (not including your calculator!).

1. 

   

   

   

2. 

   

   

3. 

   

   

   

   

   

4. 

   

   

   

   

   

   

   

   Alternatively,

   

   

   

   

   (same thing!).

5. 

   

   

  
Figure 1: Four polar plots

Problem 2 (10 pts). Match the plots shown in figure (1) to one of the following polar equations. Indicate the direction of the motion as increases.

If we number the plots by quadrant (that is, the top right is I, top left II, bottom left III, and bottom right IV), then the matches are given below. All motions are in the counter-clockwise sense.

1. - IV. This is the only unbounded function.
2. - none
3. - II - it passes through Cartesian point (1,0)
4. - I - it passes through Cartesian point (2,0)
5. - III - multiple passes through the origin.

Problem 3 (5 pts). Given these trigonometric identities

deduce the following half angle and double angle formulas:

1. 

   

   using Pythagoras ( ) we conclude that

   

   and hence that

   

   so that

2. 

   Similarly,

   

   so

   

   from which we conclude that

3. 

   

Problem 4 (10 pts). Recall that the parametric equations of the cycloid are

Set up, simplify, and solve an integral for the length of one arch of the cycloid. Show your work!

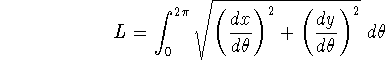
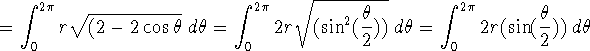
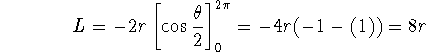
Problem 5 (5 pts). Demonstrate that the surface area of a unit sphere is .

The surface area of the unit sphere is given by rotating the top half of the unit circle about the x-axis. The equation is given by

and we use the surface area formula

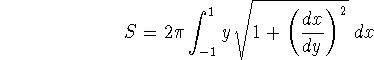
Hence

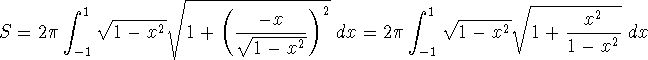
Problem 6 (5 pts). Find the partial fraction expansion of

by hand. Show your work!

Multiplying through by the denominator, we get

Equating coefficients on the left and right sides, we find that

or

Problem 7 (5 pts). Find the area of the region that lies inside the cardioid and inside the third quadrant.

  
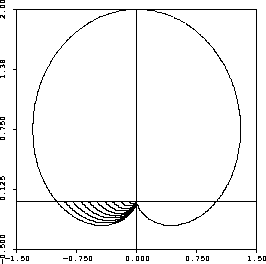
Figure 2: Problem 7: Only the third quadrant is needed.

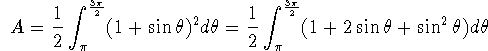
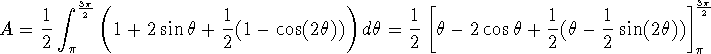
Problem 8 (10 pts).

Part I (5 pts). Plot the following points, expressed in polar coordinate, and give their cartesian coordinates: , , and

  
Figure 3: Problem 8: Three Polar Points.

Using the formulae

 

it's easy to show that the three points are given by

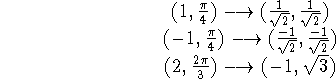
Part II (5 pts). Write the equation of the line which passes through the (Cartesian) points (0,1) and (2,3) in polar coordinates.

This is the line with slope 1 passing through (0,1), so it has Cartesian equation y=x+1. Using the equations (1), we obtain

or

Problem 9 (10 pts).

Part I (5 pts). Find the exact points on the curve given by the following parametric equations where the tangent is horizontal or vertical.

We differentiate these equations to give

and wherever these two are zero, we have the possibility of horizontal ( and vertical ( ) tangents. Thus, there will be horizontal tangents at

and vertical tangents at

Part II (5 pts) Find the tangent line to the parametric curve above when t=1. Sketch the curve (you may use your calculator) and this tangent line.

The equation we get from Figure (4): it's horizontal, with equation y=-2. See the plot.

  
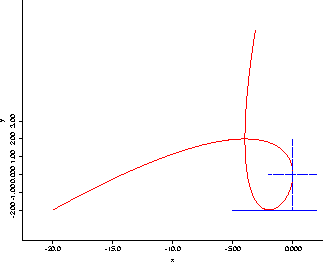
Figure 4: Problem 9: Parametric plot.

Problem 10 (10 pts). Approximate (by hand - i.e. show the coefficients)

using

1. the left rectangle rule with n=4,
2. the right rectangle rule with n=4,
3. The trapezoidal rule with n=4,
4. The midpoint rule with n=4, and
5. Simpson's rule with n=8.

 
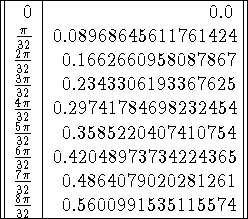
Table 1: The data needed for these rules.

 
Table 2: The results of these rules.

Recall that once the LRR and RRR results are known, the trapezoidal result is simply the average of the two.

Also, once the trapezoidal and midpoint results are known, Simpson's rule (for n twice that of trap and mid) is known as well, as the weighted average: S_2n=(T_n+2M_n)/3.

Hence only three results need to be computed directly: LRR, RRR, and Midpoint; the others can be deduced.

Problem 11 (5 pts). The cubic Bezier curve is a parametric curve on the interval [0,1] determined by 4 control points, call them , , , and . Draw the positions of these control points in order to create a reasonable semblance of the letter ``C''. Indicate (roughly, but sensibly) how the Bezier curve would look relative to these control points. Pay particular attention to tangents to the curve at and .

  
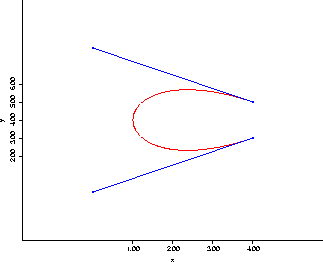
Figure 5: Problem 11: A ``C'', with slopes.

See figure (5).

• About this document ...