Name:

Directions: Show your work! Answers without justification will likely result in few points. Your written work also allows me the option of giving you partial credit in the event of an incorrect final answer (but good reasoning). Indicate clearly your answer to each problem (e.g., put a box around it). Good luck!

Problem 1 (10 pts). Given the equation of the plane

1. (6 points) Draw the plane in a suitable three dimensional coordinate system. Clearly indicate the coordinate axes x, y, and z, and the unit vectors , , and .

   To draw this, I found the intersections of the plane with the coordinate axes: (1,0,0), (0,3,0), and (0,0,2).

2. (2 points) Find a point on the plane, and indicate its location in your drawing.

   How about the point (1,0,0)!

3. (2 points) Find a unit vector perpendicular to this plane, and draw it extending from the point you chose in part 2.

   We can use the normal vector of the plane ( ), and turn it into a unit vector by dividing by its norm:

   

  
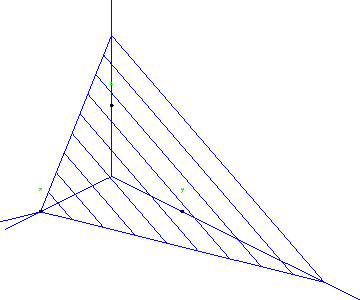
Figure 1: Problem 1: The plane and unit vector at point (1,0,0) on the plane.

Problem 2 (10 pts). A few equations:

1. (5 points) Write the equation of the sphere of radius 4 with center (3,1,6).

   

2. (5 points) Write an equation for the plane perpendicular to the xy-plane passing through the points (0,0,1) and (1,1,1).

Inspection is the easiest method! The solution is x=y. You can see this since it must be independent of z (perpendicular to the xy-plane), and since it passes through x=0=y and x=1=y (so it contains the line x=y).

To do it the harder way: we've got two points in the plane, and need a normal vector. Another point on the plane is (0,0,0) (since it's perpendicular to the xy-plane). Thus a normal is

Hence an equation of the plane is

or

Alternatively, one could find two vectors lying in the plane and provide a parametric equation for the plane: the three points provide vectors and , so

works as well.

Problem 3 (20 pts).

1. (8 points) Draw the space curve with parametric equations given by

   

   from an eye position sighting along the vector towards the origin (that is, projecting onto the vectors and ).

     
   Figure 2: Problem 3: The projection of this space curve.
   

2. (4 points) Show that the motion occurs on a sphere.

   Inspection of the equations indicates that a good idea would be to consider the squares of the coordinates:

   

   From this we see that

   

   and then

   

3. (8 points) What is the equation of the line tangent to the curve when ?

We need to compute the tangent to the motion:

which we evaluate at :

Since ,

Problem 4 (10 pts). Match the space curves in Figure 3 to the parametric equations given below by placing the correct letter in the correct matching box for the equations.

Notes: one of the sets of equations below has no corresponding plot! Leave its box empty.

The curves are projected with the eye position along the vector .

  
Figure 3: Four space curves

1. 

   

2. 

   

3. 

   

4. 

   

5. 

   

Problem 5 (10 pts). Given and . Compute:

1. 
2. 
3. 
4. 
5. 

Problem 6 (10 pts). A particle is accelerating with . Suppose that its initial velocity is given by and it is located at initially.

1. (6 points) Find the vector function of position .

   

   

   

   

   

   

2. (4 points) Describe the motion. What are the tangential and normal components of the acceleration?

   This is uniform circular motion in the xz-plane. The acceleration is entirely normal, as the speed is constant ( ).

Problem 7 (10 pts).

Find the point at which the line

intersects the plane

We simply solve (1+t) + (2t) + (3t)=1 for t, yielding t=0! Thus, the point at which the line intersects the plane is given by (1,0,0).

Problem 8 (10 pts).

1. (5 points) What is the meaning of curvature? What does large curvature mean for a space curve? Small curvature? Can you draw a picture to make its meaning clear?

   The curvature is defined as || , where s is arclength. This makes it the norm of the instantaneous change in the unit tangent vector with an infinitesmal change in arclength.

   Intuitively, it corresponds to the ``curviness'' of a space curve: the more bent the curve is, the greater the curvature. A circle of radius r has curvature 1/r, and to a curve at any point we could trace an ``osculating'' circle. This ``kissing'' circle would give the same curvature as the space curve at that point.

   A straight line has the smallest (minimal) curvature - zero.

     
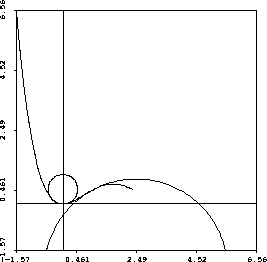
   Figure 4: Problem 8: Curvature at two points on a curve, illustrated by the osculating circle (at t=0 and t=1).
   

2. (5 points) Given . Compute the curvature using the formula

   

   

   

   

   so

   

Problem 9 (10 pts). Determine whether the following expressions make sense or not. Indicate either N (nonsense), S (scalar), or V (vector) in the box at left.

1. 
2. 
3. 
4. 
5. 

• About this document ...