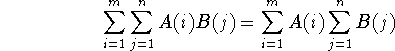Section 1.4: Predicate Logic

Abstract:

We now consider the logic associated with predicate wffs, including a new set of derivation rules for demonstrating validity (the analogue of tautology in the propositional calculus).

Derivation rules

• First of all, all the rules of propositional logic still hold. Whew! Propositional wffs are simply boring predicate wffs.

• Our author suggests the following ``general plan of attack'':

  • strip off the quantifiers

  • work with the separate wffs

  • insert quantifiers as necessary

  So how do we legitimately do so?

• New rules for predicate logic: in the following, you should understand by the symbol x in P(x) an expression with free variable x, possibly containing other variables: e.g.

   

  • Universal Instantiation: from 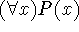deduce P(t).

    Caveat: t must not already appear as a variable in the expression for P(x): in the equation above, (1), it would not do to use P(y) or P(z), as they appear in the expression already.

    Example: Practice 21/22, p. 47/48

  • Existential Instantiation: from 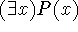deduce P(t).

    Caveat: t must be introduced for the first time (so do these early in proofs). You can do a universal instantiation which also uses t after an existential instantiation with t, but not vice versa (e.g. Example 26/27).

    Example: Ex. #5/11, p. 56/58 (start).

  • Universal Generalization: from P(x) deduce .

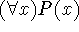    Caveats:

    • P(x) hasn't been deduced by existential instantiation from any hypothesis in which x was free, and

    • P(x) hasn't been deduced by existential instantiation from another wff in which x was free.

    Example: Ex. #11/17, p. 57/58

  • Existential Generalization: from P(a) deduce .

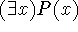    Caveat: x must not appear in P(a).

    Example: Ex. #5/11, p. 56/58 (finish).

Some results/notes

• Note that

  

  as shown on page 51, and

  

  as they suggest. This means that we can ``pass over'' predicates outside our own scope, or include them within our own scope. This is similar to what we do with summation notation, when, for example, we can write

  

• Note also the method of proof: the author introduces a temporary hypothesis. If you think about the deduction method, it takes a conclusion which is an implication and rewrites it so that the implication disappears (the antecedent becomes one of the hypotheses). Similarly, we can take an hypothesis (in this case, one which we introduce) and turn a conclusion into an implication. This is the deduction method backwards! That is, suppose that one starts with P(x) as true. You add a ``temporary hypothesis'' Q(x), and from that deduce R(x):

  

  Using the deduction method backwards, we conclude that

  

  Since P(x) implies the implication , we can add it as an hypothesis to our argument! Think about it....

  Look at the three proofs using a temporary hypothesis (Examples #30/31, and 31/32(a,b)). Notice how the introduction of the temporary hypothesis ends with an implication, which is then useful for the continuation of the proof.

  Example: Practice 24/25, p. 51/52