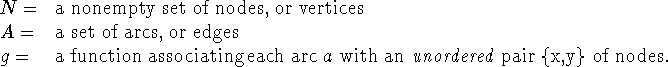
We are introduced to definitions of graphs, various kinds of graphs, characteristic features of graphs, and even a few theorems about graphs (for example, we learn when two graphs are the same, or isomorphic, even when they look strikingly different).
We then take a look at planer graphs (in particular at Euler's formula), and computer representations of graphs (adjacency matrices, adjacency lists).
A graph is defined loosely as a set of nodes, and a set of arcs which connect some of the nodes.
More formally, we have the following
Definition: a graph is an ordered triple (N,A,g) where
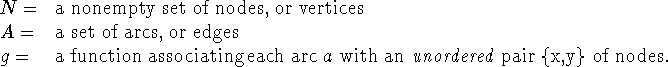
x and y are the endpoints of the arc.
g is a function 
and 
.
Example: Practice #1, p. 331/342.
Definition: a directed graph is an ordered triple (N,A,g) where
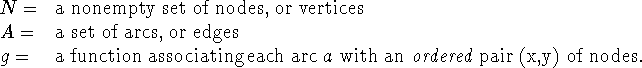
so g is a function 
and .
Example: Exercise #1, p. 351/361.
Example: Create a graph on a 4x6 card. Some of you should make rather ordered graphs; others might think of very strange graphs.
Use this graph terminology handout to classify your graph.
Example: Exercise #2, p. 351/362.
By 
we will understand the simple, complete graph with n nodes.
Example: Exercise #5a, p. 352/362: Draw 
.
A bipartite complete graph 
is a graph of N nodes which break
into two groups, 
and 
, of size m and n respectively, with the
property that two nodes x and y are adjacent 
and 
.
Example: Exercise #5b, p. 352/362: Draw 
.
The idea of isomorphism is that two structures can be ``morphed'' into each other (they are in some sense identical). Our objective, in general, is to figure out the ``morphism'' (isomorphism - same form!).
Example: Look at Figure 5.17, p. 339/350: can you morph the two graphs together?
Definition: Two graphs 
and 
are
isomorphic if there are bijections (one-to-one and onto mappings)
and 
such that for each arc 
,
(replace braces by
parentheses for a directed graph).
Example: Practice #7, p. 339/350. If you managed to morph the two
graphs in Figure 5.17, then you should be able to ``see'' the rest of function
.
Theorem: Two simple graphs and are
isomorphic if there is a bijection 
such that for any nodes
and 
of , and are adjacent 
and
are adjacent.
Example: Exercise #11, p. 353/363.
Here are some tests for determining when two graphs are not isomorphic:
Example: Exercise #8, p. 352/362.
A planer graph is one which can be drawn in two-dimensions so that its arcs intersect only in nodes.
Example: Revisit #11, p. 353/363.
Euler's Formula for simple, connected planer graphs states that
where n is the number of nodes, a is the number of arcs, and r is the number of regions (including the infinite region surrounding the graph).
Euler's formula is proven by induction, on a, the number of arcs.
Example: Revisit #11, p. 353/363.
The following theorem provides some estimates on the relationship between the number of arcs and nodes that a planer graph may possess:
Theorem: For a simple, connected, planer graph with n nodes and a arcs,
, then
and there are no cycles of length 3, then
From this theorem we can deduce that 
is not planer, since it has 5 nodes,
and 10 arcs, and 
.
Also from this theorem we can deduce that 
is not planer, since it has
6 nodes, and 9 arcs, and no cycles of length 3: 
.
Example: Exercise #22, p. 355/365.
We want to examine two different representations of graphs by a computer:
A matrix is basically a spreadsheet: a rectangular data set of numbers indexed by rows and columns.
An adjacency matrix for a graph with N nodes is NxN, where
the rows and columns of the matrix represent the vertices. If the graph is
undirected, then the element 
of the matrix is non-zero nodes
i and j are adjacent; if directed, then the element of the matrix
is non-zero there is an arc from node i to node j.
In our textbook, the element of the matrix 
, the number of arcs
meeting the criteria above.
Example: Practice #16, p. 347/358.
For an undirected graph the adjacency matrix is symmetric (which means that we can reduce storage by about half); for a directed graph, the matrix may well be unsymmetric.
Here's a nice web page, with an example.
Example: Exercise #33, p. 356/366.
An adjacency list might be a better storage method for graphs with relatively few arcs: we effectively store only the non-zero entries of the adjacency matrix, in a linked list:
Example: Exercise #46, p. 358/367.
The redundency in drawing the adjacency list for an undirected graph is evident. This is eliminated for a directed graph:
Example: Exercise #57, p. 359/367.
