Section 2.3: More on Proof of Correctness

Abstract:

In this section we add a new rule, the loop rule, to the two rules we have already concerning proof of correctness (the assignment rule, and the conditional rule).

Errata and notes

There are a couple of mistakes which we need to point out in this section:

• Exercise #12, p. 120: line 7 of code, i= should be j=.
• Exercise #13, p. 120: line 5 of code, j=a should be .

Also: for your homework, you must trace your answers to problems number 5 and 7: it is not enough to simply give the gcd of each pair!

Reminder: Proof of Correctness

``Testing can prove the presence of errors but never their absence.'' - Edsgar Dijkstra. We require proof! ``Correctness'' addresses the issue of verification - whether the program does what we intend it to do - rather than validation - what the client wants it to do.

The specification of a program can be formalized as follow:

• P : program
• X : input
• P(X) : output
• Q : precondition: predicate Q(X) on the input
• R : postcondition: predicate R(X,P(X)) on the input and the output

Now we'll agree that the program P is correct if

 

The abbreviation we will use for (1) is (a so-called Hoare triple) (named after Tony Hoare , developer of the Quicksort algorithm), where Q is the precondition and R is the postcondition.

Loop Rule

If we have a Hoare triple of the form , where s is a loop of the form

then from we can derive .

The form of the Hoare triple, , is curious, but represents two sensible facts:

• the fact that we are going to require that B' for s to terminate; and
• the fact that the iterative procedure will have some rational basis (Q) in updating the values of intermediate steps, which will be true in the end as well as in the beginning, and throughout the looping procedure.

Loops are not necessarily of this form; but those which we can prove correct will be!

The trick is in finding Q, the so-called loop invariant for a particular loop. It may be a function of any variables local to the loop, as well as any variables passed into the loop.

Example: Exercise 3, p. 118

The interesting example presented in the book is of the GCD, or Greatest Common Divisor, of a pair of integers. An algorithm (the Euclidean Algorithm, 2300 years old) dependent upon a while loop is presented. The big idea is as follows: given integers , if a and b have a common factor c, then so does their remainder:

where r<b, and and , so

Thus c divides r, just as it divides a and b.

The idea of the algorithm is thus simply to divide the larger integer a by the smaller b, then iterate this process, with

(since the remainder and the original integers all share a common factor), continuing until the algorithm terminates (when the remainder is 0).

Example: Exercise 8, p. 118

In the proof, the loop invariant Q is gcd(i,j)=gcd(a,b). We prove the algorithm correct by induction:

1. Q(0): is true, since and .
2. Assume Q(k), and consider Q(k+1):

   

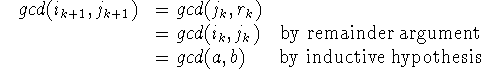
   since, as we have demonstrated, the remainder and j have the same factors as i and j.

3. Finally we check that Q is verified upon exit from the loop. At loop termination,

   

   so

   

   But gcd(i,0)=i, so gcd(a,b)=i. Therefore GCD is correct.

Example: Exercise 13, p. 120

A note on Verification and Validation

I've just got to point out that on numerous occasions in this section the author presents a problem which might be true for all real numbers, and then declares the variables as integer in her programs. This could be an example of the concern with verification, rather than validation (what the client wants). For example, Exercise #1, p. 117: ``Function to return the value of for '' only works for integers.

...

Dijkstra, whom we will meet later in the course, is also famous for his quote that ``the quality of programmers is a decreasing function of the density of GO TO statements in the programs they produce.'' (from a letter to the editor of Communications of the ACM, circa 1968)