Day 27: STA205 - Introduction to Statistical Methods

Today:

• Return Exam 3
  • Mean: 70
  • StdDev: 20
  • Curve: add 2.5 points to your total
  • You can get 20% of your lost points by meeting with me to go over your exam. For example, if you got a 60, you can get .2*(100-60)=8 points by meeting to go over the exam.

  • I need the tests back to do some more analysis -- you'll get them back for good on Thursday.

• Quiz next time over the Chi-square distribution (today's topic)

• Nice example of 2-way ANOVA (basically, the idea is that we introduce additional factors as independent variables)

• Section 12.1: Comparing two qualitative variables: the chi-square test
  • How could we determine if men, women, and children have the same opinion of four breakfast cereals? We might do a survey, collect data, and then make a statistical answer. What would lead us to say that they have the same opinion?

  • One approach:
    Data is summarized in a contingency table, with one variables' levels across the top (e.g. men, women, children) and with the other variables' levels across the side (e.g. Cereal A, Cereal B, Cereal C, Cereal D). The cells might contain the counts of those who pick that cereal as the best (ties not permitted).

    	Men	Women	Children
    Cereal A	9	12	15
    Cereal B	25	30	19
    Cereal C	35	25	20
    Cereal D	31	33	46

  • We might also include row and column totals in the table. There will be some dependency in the counts.

    	Men	Women	Children	Total
    Cereal A	9	12	15	36
    Cereal B	25	30	19	74
    Cereal C	35	25	20	80
    Cereal D	31	33	46	110
    Total6.4	100	100	100	300

  • Chi-square test: A test for dependence of two variables (p. 495)
    Decision rule: Accept H_a if p-value < Test Statistic:

  • Conditions of using a chi-square test (p. 496):
    • The sampled data must be obtained by
      1. Selecting a random sample of the population of interest, or
      2. Selecting random and independent samples for each level of one of the variables.
    • All expected cell counts must be greater than or equal to 5.

  • The chi-square distribution
    • Is skewed right:

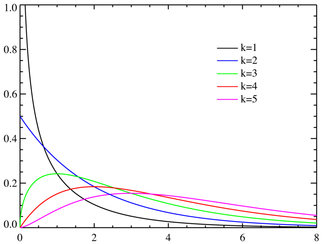
    • Calculation requires knowing degrees of freedom ("k" in the plot above; df=(R-1)(C-1), where R is the number of levels of one variable and C is the number of levels of the other)

    • Large values of chi-square signify that it's unlikely that the the variables are independent (reject the null!). As you can see, p-values are in the right tail area:

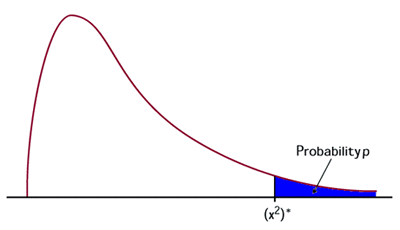
    • To get an idea of what is "large", the mean of the chi-square is df, and the standard deviation is the square root of 2*df.

  • Examples:
    • Here's how to do a chi-square in StatCrunch (Exercise 1, page 503): http://www.nku.edu/~statistics/data/c12s01e01.xls

    • Let's look at the book example, Example 12.1, p. 496, in StatCrunch: http://www.nku.edu/~statistics/data/exam12-01.xls

    • Here's the cereal example: http://www.nku.edu/~longa/classes/sta205/days/day27.txt

    • Important note: dependency does not mean that one variable determines the other.

    • Let's look at the web example: from the course website

• Section 12.2: Describing the relationship: sample percentages
  • The web example above leads us into section 12.2. Once the chi-square test indicates that there is dependence in the variables, we want to have an easy way to describe it, and sample percentages is the easiest way.

  • Note: we do not perform the chi-square test on the percentages, but rather on the actual data collected instead. If we do not detect a dependency, then we do not move to the discussion of the differences in percentages.

  • Let's return to Exercise 1, page 503/509: http://www.nku.edu/~statistics/data/c12s01e01.xls

• StatCrunch
• t-table
• Z-table
• Scientific calculator