- Section 12.1 returned: graded #12 and 40.
- Sean recommends "justmathtutoring.com" videos for help.
- Section 12.2 problems are due tomorrow.
- Change in plans: Section 12.3 problems: one of them will appear on the exam -- okay?
- I already indicated above what the speed should be -- so I'm not
going to spend much time on that.
How can we use this formula, however? Suppose a particle has followed the parametric curve C(t)=(x(t),y(t)): then we can compute how far the particle has travelled during the interval
easily using the dirt formula, d=rt (in its modified form
).
In this case, the rate is just the speed. So we compute the integral
This is actually just a re-expression of the arc length formula:
and
.
But arc length may be different from the distance the particle travelled: a particle can revisit many sections of the curve y(x) -- so once again we need to be careful to distinguish between the independent variable of interest (whether x or t).
- Other calculations can be generalized. For example, the formula
for surface area:
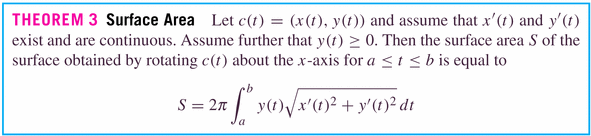
- Examples:
- #2, p. 620
- #13, p. 620; and let's start by developing the equations for the cycloid.
- #14, p. 620
- #21, p. 620
- #36, p. 621
- Homework: one of these will appear on the exam: pp. 627-630, #4, 6, 8, 9, 10, 13, 14, 22, 25, 31, 50, 51
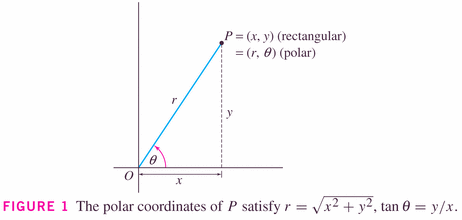
- We're going to be using a different coordinate system to
describe points in the plane -- no big deal, except that you're quite
likely unfamiliar with the new system (called polar
coordinates):
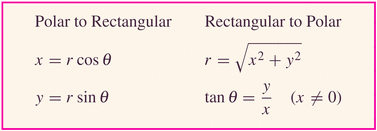
Coordinate r is called the radial coordinate and
is called the angular coordinate.
Notice something interesting: what are the radial coordinates of (x,y) and (-x,-y)?
(See the constraints on
on page 627)
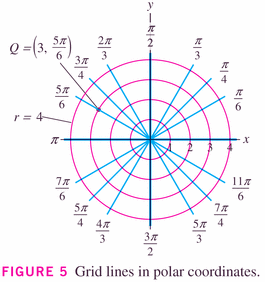
- If horizontal and vertical lines are very easily expressed in the
usual Cartesian coordinates system, it's circles and lines centered at
the origin that are easily expressed in polar coordinates. Here are the
"grid lines" in polar coordinates:

- One of the problems of polar coordinates is their non-uniqueness:
We can sometimes use that to our advantage, however; for example, if we want to imagine a point travelling around a circle, then
is a parameter, and by letting it run over multiples of
the point makes multiple trips around the circle....
- We sometimes permit r to be negative, too, for
convenience. In terms of non-uniqueness we also have that
- One of the advantages of polar coordinates is that they allow us
to create curves that can't be represented as functions of Cartesian
coordinates y(x).
- Examples:
- Understanding polar coordinates:
- #1, p. 627
- #2, p. 627
- Converting between coordinate systems:
- #3, p. 627
- #5, p. 628
- #20, p. 628
- Converting equations:
- #16, p. 628
- #20, p. 628
- #33, p. 629
- Deriving equations in polar coordinates:
- a line passing through (x,y)=(a,b) with slope m
- Understanding polar coordinates: