- Don't forget Friday's lunch. Be ready!
Join us for the next Department of Mathematics Major/Minors Lunch.
When: Friday December 5, 2008, 11:30am-1:30pm
Where: ST 343 (the Calculus Lab)
All mathematics majors and minors [and even prospective ones!;)] are welcome. This is a great opportunity to get together with other students and faculty on a very informal basis. Plus, the food is good. - I just want to apologize for all the physics you're going to see, for you non-physicists. It just turns out to be a really handy context for this discussion!
- Objectives:
- Introduce the definitions and rules of vectors
- Use vectors to represent objects in two and three-d (e.g. lines, planes).
- Use vectors to represent motions in space, and the associated quantities such as accelerations, forces, etc.
- Use certain vector notions (e.g. dot and cross products) to represent things more easily.
- Sections 13.1 and 13.2 basically define and treat vectors in two-
and three-dimensional spaces.
- Uniform Circular Motion is well-understood using the concepts of vector geometry.
- remember that
and
- The three vectors that are (most) important are the
vectors of
- position,
- velocity, and
- acceleration.
- For all of the gory details, a nice layout of all the physics, and a cool example, let's check out physclips -- the Australian dialect makes it more fun, too!
- remember that
- vector: a quantity with length and direction:
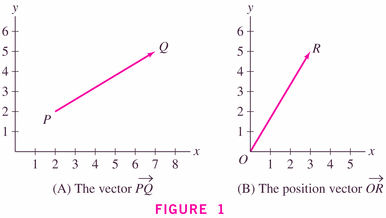
If the vectors are in two-dimensions, then the lengths are just given using the Pythagorean theorem formula:

or, for position vectors of the form
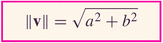
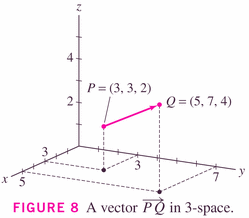
in which case
or
Obviously this can be generalized to vectors in four dimensions, five dimensions; even six dimensions. Maybe seven dimensions, too; or even n dimensions.
- Vectors with length 1 are special, called unit
vectors, and are important because they can be dedicated to
showing direction:
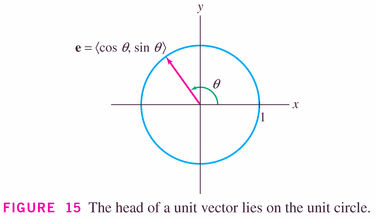
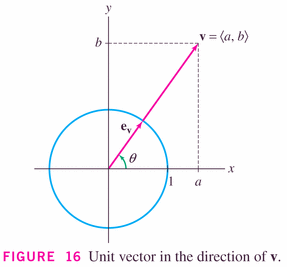
It's clear that we can turn any vector into a unit vector, by simply scaling it:

- The vectors above are given with components:


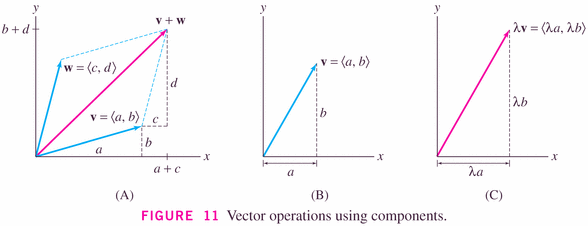
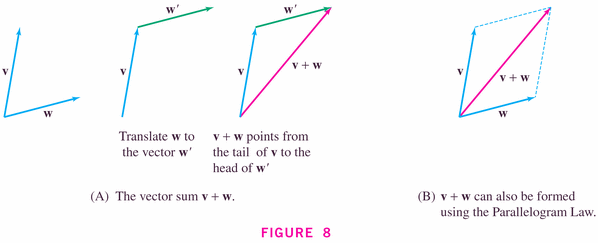
- Figure 11 illustrates the so-called parallelogram rule:
Here it is in three-space:
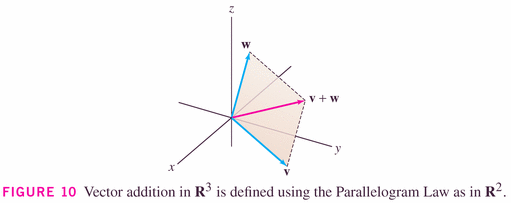
with the obvious changes to formulas because you now have three components, instead of two:
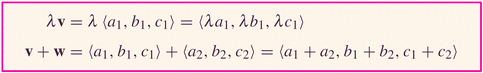
- We use special components and the parallelogram rule to write each vector in terms of a basis of vectors (equal in number to the dimension of the space): for example,
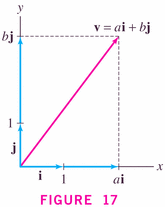
and, in three-space,
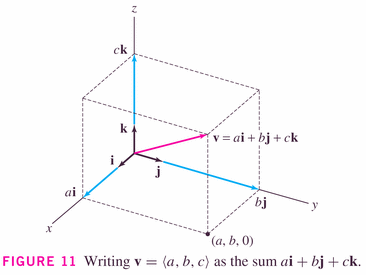
- Theorems:

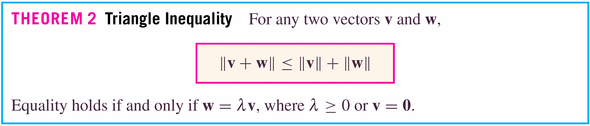
This rule is familiar in the form of the old algebraic inequality
- Let's look at some examples:
- #5, p. 663
- #9, p. 663
- #17, p. 664
- #37, p. 664
- Now, let's look at another example from physics, that makes use of
several of these ideas: #58, p. 665
- First and foremost: Newton's laws of motion (in particular
), and statics.
- The parallelogram rule
- We can think of the force vectors on the cables as being composed of vector components (as well as coordinate components).
- First and foremost: Newton's laws of motion (in particular
- Homework problems: pp. 665-, #22, 30, 38, 59, 60; due Tuesday, 12/9.
- Uniform Circular Motion is well-understood using the concepts of vector geometry.
- Differentiating vector-valued functions is (may be!) much like differentiating scalar functions. As another example, we might revisit #13, section 12.4, to see how to use the vectors to see which direction we're heading.
- Parametric equations of lines. Let's revisit uniform circular motion. As we saw in that case,
and
Now, let's "cut the string", and watch the ball fly. We had a formula for the trajectory, but now it's no longer in uniform circular motion. If there is no other force on the ball (e.g. we do this experiment in deep space), then it will fly off in a straight line. How can we represent this line parametrically?
Suppose that the string is cut at
.
- Where's the ball, and in what direction will it travel?
- How can we represent this?