Day 53 in MAT229

Last time: Section 13.1/13.2

Next time: Section 13.3/13.4

Today:

Announcements:
- Quick! Go get lunch!
- Homework problems:
  - pp. 665-, #22, 30, 38, 59, 60 (due Tuesday, 12/9).
  - pp. 673-674, #13, 18, 22, 26, 45, 50, 51 (due Thursday, 12/11).
  - pp. 680-683, #2, 7, 8, 14, 16, 41, 42, 60, 70, 71 (due Friday, 12/12).
- A problem or two from 13.4/13.5 will appear on the final.
Vector Geometry
- We were looking at example #58, p. 665:
  - First and foremost: Newton's laws of motion (in particular ${\underline{\bf{F}}=m\underline{\bf{a}}}$ ), and statics.
  - The parallelogram rule
  - We can think of the force vectors on the cables as being composed of vector components (as well as coordinate components).
  It turns out that we could see the solution very easily; calculating the force vectors was a little more complicated.
  Now let's think a little more about how we resolve the vector forces into components: we'll find it convenient to define a product of two vectors as follows:
  
  (how would you define this for vectors in two-space?). It's just component-wise multiplication, and we add up the results.
  It turns out that
  
  where
  
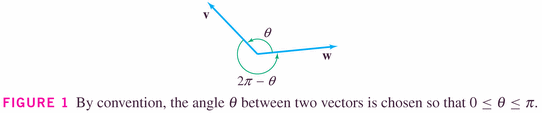
  Otherwise, the angle is acute.
  
  Finally then, we can put it all together to get this:
  
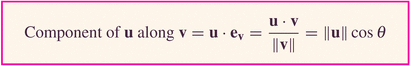
  Let's use the dot product, then, to write the components in the x and y directions of these forces.
- Differentiating vector-valued functions is (may be!) much like differentiating scalar functions. As another example, we might revisit #13, section 12.4, to see how to use the vectors to see which direction we're heading. Let's use this applet to help us visualize the situation.
- Parametric equations of lines. Let's revisit uniform circular motion. As we saw in that case, ${\underline{\bf{v}}=\frac{d\underline{\bf{r}}}{dt}}$
  and
  
  ${\underline{\bf{a}}=\frac{d\underline{\bf{v}}}{dt}}$
  Now, let's "cut the string", and watch the ball fly. We had a formula for the trajectory, but now it's no longer in uniform circular motion. If there is no other force on the ball (e.g. we do this experiment in deep space), then it will fly off in a straight line. How can we represent this line parametrically?
  Suppose that ${\underline{\bf{r}}(t)=\langle{\cos(t),\sin(t)\rangle}}$ , and that the string is cut at time ${t=t_0}$ .
  - Where's the ball, and in what direction will it travel?
  - How can we represent this?

Website maintained by Andy Long. Comments appreciated.