Day 55 in MAT229

Last time: Section 13.3

Next time: Section 13.4/13.5

Today:

Announcements:
- I made a change in how I curve the last test: I'll give you 20% of the difference between your score and a hundred (to motivate those who did well to come in, perhaps!;). It gives everyone a little boost, too.
- According to the exam schedule, you all should be free from 1:00-3:00 on Tuesday, 12/16. I'll plan to hold a review session then (which will include a chance for you to ask problems about any of the topics we've covered.
- I also plan to hold a review session Thursday, 12/18, in the evening. Let's say 7:00-9:00 (or until everyone is gone!;)
- HW12.4 Returned:
  - #18: limits of integration: 0, 3 (where does the radius equal zero?)
  - #24: limits of integration: 0, $\pi$ (if you to $2\pi$ , you'll make two trips around the circle!)
- Reminder: Homework problems:
  - pp. 665-, #22, 30, 38, 59, 60 due today.
  - pp. 673-674, #13, 18, 22, 26, 45, 50, 51 (due Thursday, 12/11).
  - pp. 680-683, #2, 7, 8, 14, 16, 41, 42, 60, 70, 71 (due Friday, 12/12).
- A problem or two from 13.4/13.5 will appear on the final.
- Something fun(ction):
  - Google Trends!
  - What features do we focus on?
  - These are the functions you will find yourselves working on....
Vector Geometry
- We considered parametric equations of lines last time, again starting from uniform circular motion. As we saw in that case, ${\underline{\bf{v}}=\frac{d\underline{\bf{r}}}{dt}}$
  and
  
  ${\underline{\bf{a}}=\frac{d\underline{\bf{v}}}{dt}}$
  But that ${\underline{\bf{v}}\cdot\underline{\bf{r}}=0}$ and that ${||\underline{\bf{v}}||=||\underline{\bf{r}}||}$ .
  If we "cut the string" holding the particle (or planet!) in uniform circular motion, then the equation of the line along which it would move to be the following:
  
  Examples:
  - #46, p. 674 (another way to tell that they're the same line)
  - #52, p. 674 (in what plane do these two lines lie?)
- Section 13.4: The Cross Product
  - The next product we'll find convenient to define is the cross product, which is a product of two vectors resulting in a third vector, which juts into the space perpendicular to which the two vectors live. It is only useful in three-space, which makes it somewhat unusual (the dot product exists and is useful in any-dimensional space).
    Because the cross product is linear in the components, we can define it on the unit vectors in three space, and then deduce it using the component-wise definition of a three-vector.
    
    ${\hat{i}\times\hat{j}=\hat{k}}$ ${\hat{j}\times\hat{k}=\hat{i}}$ ${\hat{k}\times\hat{i}=\hat{j}}$
    
    When you reverse direction, however, you get ${\hat{i}\times\hat{k}=-\hat{j}}$ ${\hat{j}\times\hat{i}=-\hat{k}}$ ${\hat{k}\times\hat{j}=-\hat{i}}$
    
    Property (i) of the basic properties is called anti-commutativity. Property (ii) shows that we can use the cross-product as a test for parallelism (rather than perpendicularity, which is the job of the dot product).
    
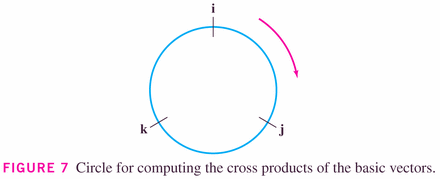
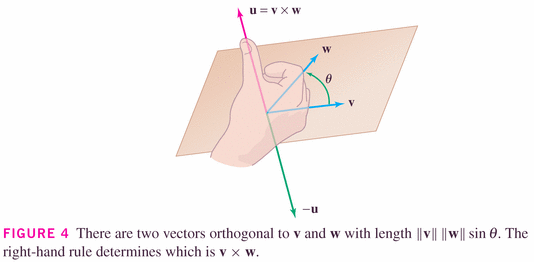
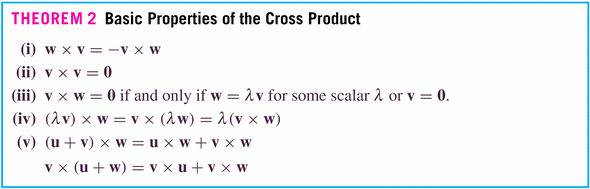
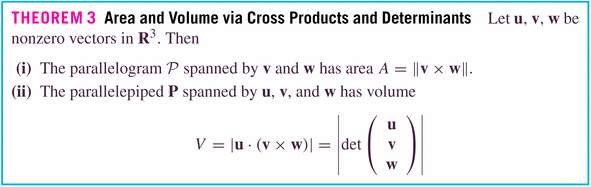
    Don't worry about the determinant stuff in these sections: we'll leave that to linear algebra! It's an interesting little side-trip at this point, but becomes fundamental in LA.
    Examples:
    - #20, p. 691
    - #28, p. 691
    - The force ${\bf{F}}$ on a proton moving at velocity ${\bf{v}}$ (in m/s) in a uniform magnetic field ${\bf{B}}$ (in teslas) is ${\bf{F}=q(\bf{v}\times\bf{B})}$ (in Newtons), where ${q=1.6\times{10^{-19}}}$ Coulombs:
      
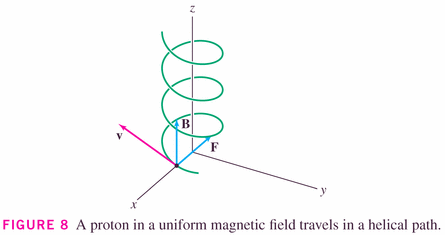
      Time for a little calculus, differential equations, and linear algebra:
      Let's see if we can deduce the trajectory of the proton in this illustration.
    - #36, p. 692
    - A great explanation of torque: #64, p. 693
    Links:
    - Another look at the cross product

Website maintained by Andy Long. Comments appreciated.