Day 57 in MAT229

Last time: Section 13.4

Next time: The Final!

Today:

Announcements:
- Don't forget to do your on-line Course Evaluations: eval.nku.edu.
- There will be review sessions:
  - Tuesday, 12/16, 1:00-3:00 pm
  - Thursday, 12/18, 7:00-9:00 pm
- HW13.2 Returned:
  - #13
  - #18
- Homework pp. 680-683, #2, 7, 8, 14, 16, 41, 42, 60, 70, 71 is due today (I'll have it by Monday, posted on the door of my office).
- A problem or two from 13.4/13.5 will appear on the final, from the following list:
  - pp. 692: #36, 38, 53, 65
  - pp. 699: #4, 14, 25, 33
- The final will be about 30% new stuff, 70% old. You'll be allowed to skip one or two of the "old stuff" problems. Best way to study: review your tests (be able to do every problem). If you can do that, you should be in good shape. I'll be asking similar problems.
Vector Geometry
- Today our mission is to finish up the vector stuff. There are two things I want to do:
  1. talk about torque (and how to use mathematical relationships to derive the notion); and
  2. see how to use the cross-product to write equations of planes in parametric and non-parametric forms.
- Here is a great explanation of torque.
  - Torque is work to create rotation (work in the technical sense: force times the distance through which the force is applied).
    Think about a wrench: if you want to create rotation (twist off a nut), how should you apply your force?
    The nut is at the origin of our system, and we want to create rotation there. So ${\bf{r}}$ is the vector from the nut to the position at which we apply the force (where our hand contacts the wrench).
    How can you increase your torque?
    How is it affected by the angle ${\bf{\theta}}$ , vector ${\bf{r}}$ , and vector ${\bf{F}}$ ?
  - #64, p. 693
- Equations of Planes
  - We'll start with planes through the origin: general planes are just displaced versions of these.
  - Thus, the vectors I discuss in the next few lines can be considered position vectors, originating from the origin.
  - The parallelpiped equation in Theorem 3
    
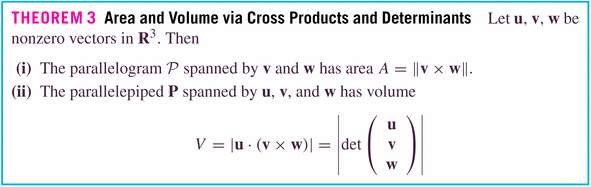
    gives us a hint as to how to write the equation of a plane containing ("spanned by") two vectors ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ : We want to find all vectors ${\underline{\bf{u}}}$ living in the space. Those will be the ones such that
    
    ${\underline{\bf{u}}\cdot(\underline{\bf{v}}\times\underline{\bf{w}})=0}$
    I.e., ${\underline{\bf{u}}}$ creates a zero volume parallelpiped, because it's living in the same space as ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ .
    This gives us our first equation of a plane: if the coordinates of ${\underline{\bf{u}}}$ are given by ${\langle{x,y,z}\rangle}$ and the coordinates of ${\underline{\bf{v}}\times\underline{\bf{w}}}$ are given by ${\langle{a,b,c}\rangle}$ , then the equation becomes
    
    ${ax+by+cz=0}$
    This is one form of the equation of a plane (through the origin). We say the the cross product is normal to the vectors that live in the plane (or normal to the plane): that is, that it is perpendicular to the plane.
    
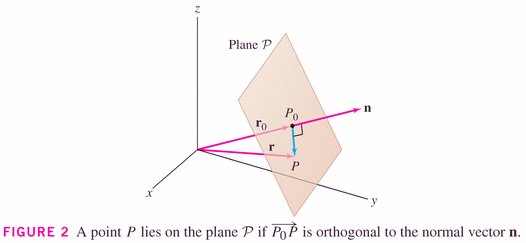
    Now (for the second equation!): notice that ${\underline{\bf{u}}=s\underline{\bf{v}}+t\underline{\bf{w}}}$ satisfies the equation of the plane ${\underline{\bf{u}}\cdot(\underline{\bf{v}}\times\underline{\bf{w}})=0}$ , since ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ are both perpendicular to their cross product. Hence we have another (parametric) equation of a plane (through the origin):
    ${\underline{\bf{u}}(s,t)=s\underline{\bf{v}}+t\underline{\bf{w}}}$
  - To offset these planes from the origin, one needs only reinterpret in the two forms of the equation:
    1. ${\underline{\bf{u}}=\underline{\bf{r}}-\underline{\bf{r}}_0=\langle{x,y,z}\rangle-\underline{\bf{r}}_0}$
      which leads to
      
      ${(\langle{x,y,z}\rangle-\underline{\bf{r}}_0)\cdot\langle{a,b,c}\rangle=0}$ or ${ax+by+cz=d}$
    2. ${\underline{\bf{u}}=s\underline{\bf{v}}+t\underline{\bf{w}}+\underline{\bf{r}}_0}$
      which leads to
      
      ${\underline{\bf{u}}(s,t)=s\underline{\bf{v}}+t\underline{\bf{w}}+\underline{\bf{r}}_0}$
  - Examples:
    - #12, p. 699
    - #29, p. 700
    - #30, p. 700
  Links:
  - Another look at the cross product

Website maintained by Andy Long. Comments appreciated.