- Thanks to Dylan for an emailed couplet
- If interested, I found a sermon written by Charles's father at Google Books, from 1838. I haven't read it yet!
- Memoria Technica Couplets
- and their use in mathematics: the logarithm.
- Elections -- Dodgson becomes an administrator, and hence has to
deal with decision-making at the university. You'll find
yourself remembering his plight some day!
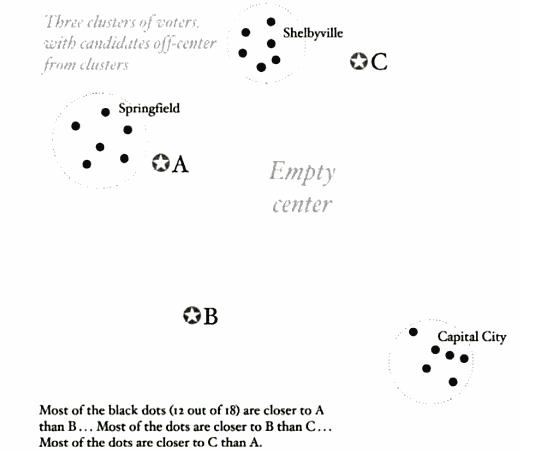
- The Colas versus the UnCola
- Simple Majority -- p. 133
- Method of Elimination -- p. 133
- Method of Marks
- Method of Marks (revised) -- p. 135
- A Method of taking votes on more than two issues (preview)
-
- Section 8.4 of the Heart of Mathematics: Peril at the Polls
- Sixth grade vice-presidential vote
6 boys prefer 4 boys prefer 8 girls prefer 4 girls prefer First Choice Chad Chad Gwyn Courtney Second Choice Courtney Gwyn Courtney Gwyn Third Choice Gwyn Courtney Chad Chad Three voting schemes, three different winners.
- Plurality voting -- Chad wins
- Vote for Two -- Courtney wins
- Borda Count Method -- Gwyn wins
- Here's my favorite system: Instant run-off, until we have a majority. Who wins?
Look, it seems like this should be easy. We want a system that has the following properties, given each voter's list of ordered rankings for the candidates:
- Better is better: If a voter changes his or her vote in favor of Candidate X, then that shouldn't hurt Candidate X.
- Ignore the irrelevant: throwing out a loser will not change the outcome.
- Go along with the consensus: if everyone agrees, then we have a winner.
Here's the main, astonishing result:
The only voting scheme that satisfies these three very reasonable requirements is a dictatorship! That is, one person makes the decision.
It was not a "fluke" that different methods gave different results. As mentioned in the text, mathematicians can "rig" a seemingly benign system that will hand the election over to a preferred candidate.
- "Transitivity" means that, if we prefer A to B, and B to
C, then we'll prefer A to C. Condorcet's Paradox says there's
no promise of transitivity!
Example:
5 voters' ranking 5 voters' ranking 5 voters' ranking First Place A B C Second Place B C A Third Place C A B Look at the beautiful symmetry in this table.... It's responsible for the problem, in many ways.
- I want to share a story from my days in the Peace Corps in Togo.
- Sixth grade vice-presidential vote
- Lawn Tennis Tournaments
- See the (bad) scheme on page 143.
- We consider the scheme in which 8 players play each other so that the top three players are not knocked out prematurely, then how can we proceed?
- Lawn Tennis Tournaments: The True Method of Assigning Prizes with a Proof of the Fallacy of the Present Method (p. 143)
Carroll basically proposes double-elimination tournaments.
- Parlimentary Representations
- Principles of Parliamentary Representation
- His work is considered a brilliant contribution.
- What new things do we learn about Dodgson in this Fit?
- At work
- At "play"
- Ariel's Song from The Tempest
Full fathom five thy father lies;
Of his bones are coral made;
Those are pearls that were his eyes:
Nothing of him that doth fade,
But doth suffer a sea-change
Into something rich and strange.
Sea-nymphs hourly ring his knell:
Ding-dong.
Hark! now I hear them -- Ding-dong, bell.
- Ariel's Song from The Tempest