- Your homework for section 11.3 is due today.
- Homework for 11.4 has been pushed back to 10/29.
- Homework for 11.5 will also be due 10/29.
- Exam revisions are not graded yet -- sorry.
- Read Section 11.6 for next time responding to the worksheet for section 11.6.
-
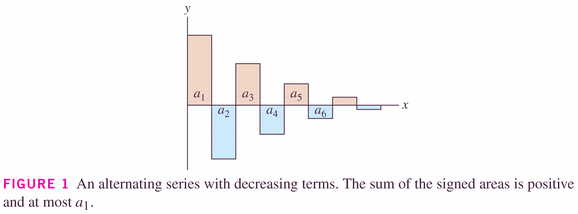
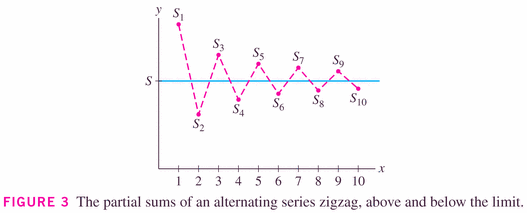
Once again, our mission here is not necessarily the value of the
series, but may be simply knowledge of whether it converges or
not.
That being said, Theorem 2 below does give us some help in determining the value of (or at least bounds on the value of) the series.

- Series that converge absolutely, and
- Series that don't.


- Examples:
- #2, p. 570
- #6, p. 570
- #8, p. 570
- #18, p. 570:

is the size of the term (i.e. positive).
- #27, p. 570
- It turns out that conditionally convergent series can have their terms rearranged to converge to any limit you like. Hmmm.... Is this the end of commutativity?!
- There are two main results (theorems) in section 11.5. They are
two tests for convergence of series:

This result says that eventually the ratio of successive terms is effectively constant,
: what kind of series looks like that? A geometric series:
- #1, p. 574
- #5, p. 574
- #8, p. 575
- #13, p. 575

This result says that eventually the absolute values of the terms are effectively equal to
: what kind of series looks like that? A geometric series!
No wonder the results of the tests look exactly the same.... Too bad Rogawski didn't just use the same letter for the limits in both cases!
Notice that, once again, limits of sequences plays an important role! Series are just sums of sequences, after all; we're focused on how terms behave (root test), how successive terms behave (ratio test), or how partial sums behave.
Examples:
- #34, p. 575
- #36, p. 575
- Pick any....
