- Your homework for section 11.3 is due next Thursday.
- Homework for 11.3 will be pushed back until 10/22.
- Homework for 11.4 will be pushed back until 10/29.
- We'll do 11.5 next time (no quiz, as I forgot to make up the worksheet!;)
- Exam revisions are due today.
-
Once again, our mission here is not necessarily the value of the
series, but may be simply knowledge of whether it converges or
not.
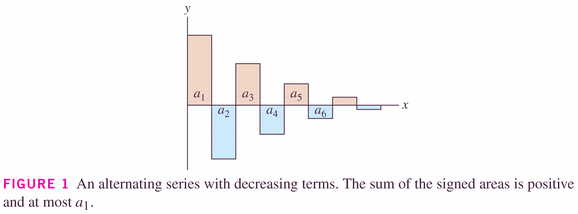
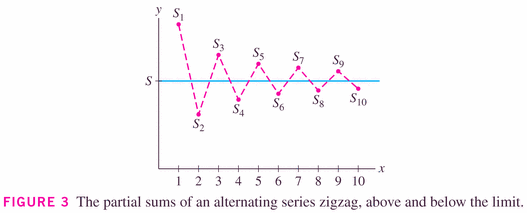
That being said, Theorem 2 below does give us some help in determining the value of (or at least bounds on the value of) the series.

- Series that converge absolutely, and
- Series that don't.


- Examples:
- #2, p. 570
- #6, p. 570
- #8, p. 570
- #18, p. 570:

is the size of the term (i.e. positive).
- #27, p. 570
- It turns out that conditionally convergent series can have their terms rearranged to converge to any limit you like. Hmmm.... Is this the end of commutativity?!
