- Your homework for section 11.2 is due today.
- Homework for 11.3 will be pushed back until 10/22.
- Read Section 11.4 for next time responding to the worksheet for section 11.4.
- Continue working on your exam revisions! (Here's another link to Exam I). These are due Thursday.
- concerns several different means of testing for convergence of
series with all positive terms (obviously, if we're dealing with series
of all negative terms, similar results are going to apply).
- We're not so concerned with the actual limits (that is the values
of the series) as we are with the convergence (or divergence) of the
series.
- Theorems:

The partial sums are terms in an increasing sequence, since the terms of the series are all positive.
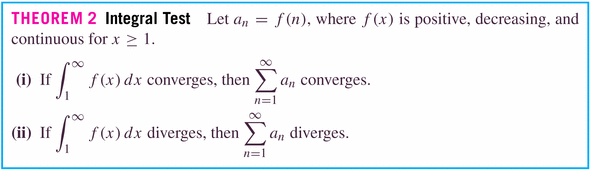
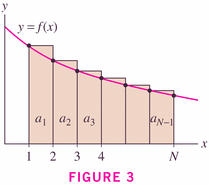
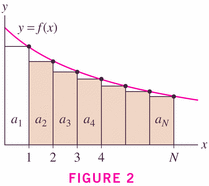
Examples of the Integral Test:
- #9, p. 563
- #10, p. 563
Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

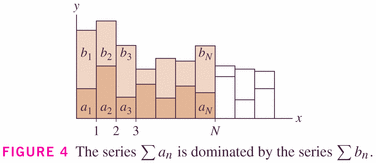
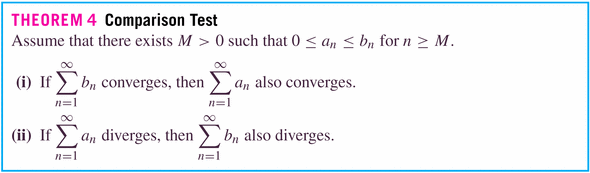
- Comparison Test: #20, p. 563

This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series. So, in the long term, one series is behaving like a scalar multiple of the other. And so if one converges, the other will, too.
Examples:
- Limit Comparison Test: #34, p. 563
- Divergence of the harmonic series (and dominoes!): #84, p. 565
-
Once again, our mission here is not necessarily the value of the
series, but may be simply knowledge of whether it converges or
not.
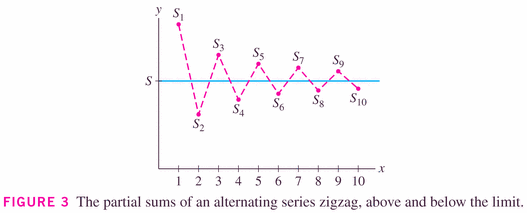
That being said, Theorem 2 below does give us some help in determining the value of (or at least bounds on the value of) the series.
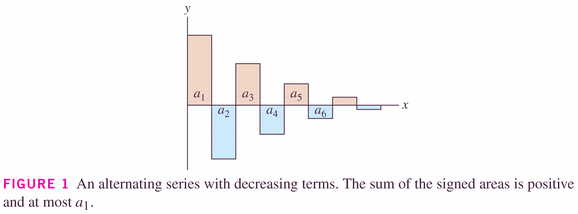

- Series that converge absolutely, and
- Series that don't.


- Examples:
- #2, p. 570
- #6, p. 570
- #8, p. 570
- #18, p. 570:

- #27, p. 570
- Is conditional convergence the end of commutativity?! Well, sort of!
