- Homework for 11.6 due.
- Homework for 11.7 due next time.
- Exam revisions graded: come in to discuss it and get 100% on the redo. Email me to schedule a meeting (Please use subject line REDO).
- Read Section 13.2 for next time responding to the worksheet for section 13.2.
- Short quiz on 13.1/13.2 next time.
- Today we start "Vector Geometry". When you're working with (and drawing vectors), it's sometimes convenient to have graph paper. I've put a link on our home page to some graph paper you can simply print off as you need it.
- Just FYI: next week (Thursday) we'll have our second exam. It will cover the rest of chapter 11 (11.2-11.7).
- We've basically seen all this material before: we're now just
summarizing:
The coefficients akare "designed" so that after k differentiations of the series, when we evaluate the series we pick off only the kth derivative evaluated at x=c:
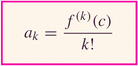

If we can bound all derivatives of a function on an interval about x=c, then the Taylor series represents the function there:

The expansion for the binomial series is a classic: it's another of the great achievements of Sir Isaac Newton, one of the founders of calculus:
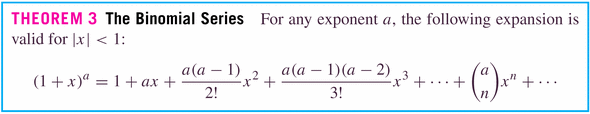
What about its radius of convergence? Let's look at #84, p. 599.
- Examples:
- #1, p. 596
- #4, p. 597 (remember that there are several different ways to do these! You don't have to work from the definition....)
- #10 p. 597
- Let's take a look at some more interesting problems....
- #48, p. 597
- #49, p. 598 (Note: if you have the First Printing of our text, you don't have this problem -- and all the rest of your problems will be off by one!).
- #77, p. 598 (homework)
- #79, p. 598
- Uniform Circular Motion is best understood using the concepts of vector geometry.
So are many other concepts from physics, where quantities have a direction and a "strength" -- a rocket in flight, for example. It is moving in a certain direction, and it has a speed, whose value can be represented by the length of a vector.
- vector: a quantity with length and direction:
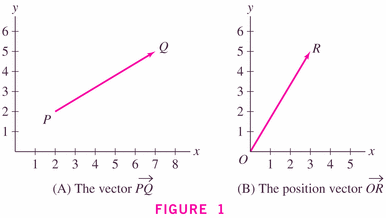
- In uniform circular motion, we could represent the position of the bob by
and
- The three vectors that are (most) important in the physics
of circular motion are the vectors of
- position,
- velocity, and
- acceleration,
- Animations, demonstrations:
- Uniform Circular Motion
- For all of the gory details, a nice layout of all the physics, and a cool (but scary) example, let's check out physclips -- the Australian dialect makes it more fun, too!
- vector: a quantity with length and direction:
- If a vector is in two-dimensions, then the length
is just given using the Pythagorean theorem formula:

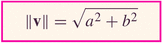
in which case
Obviously this can be generalized to vectors in four dimensions, five dimensions; even six dimensions. Maybe seven dimensions, too; or even n dimensions.
- The vectors above are given with components:

examples:
- #5, p. 663
- #9, p. 663
- #11, p. 663

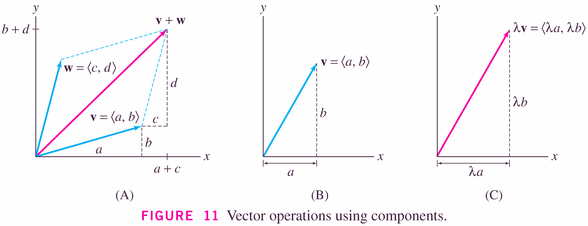
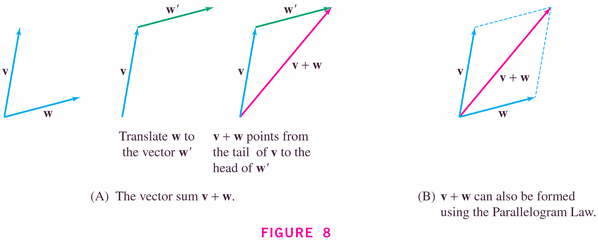
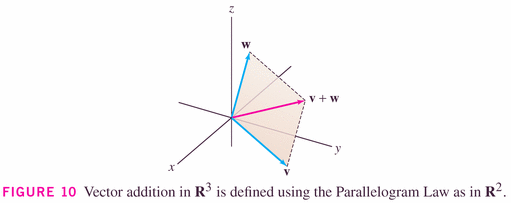
- Figure 11 illustrates the so-called parallelogram
rule:
example:
- #17, p. 664
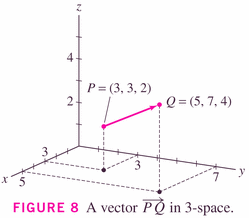
Here it is in three-space:
with the obvious changes to formulas because you now have three components, instead of two:
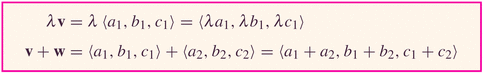
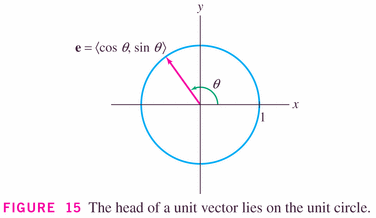
- Vectors with length 1 are special, called unit
vectors, and are important because they can be dedicated to
showing direction:
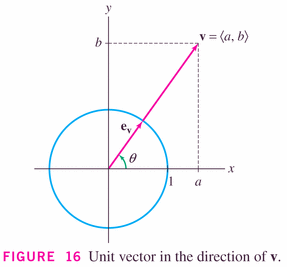
It's clear that we can turn any vector into a unit vector, by simply scaling it:

example:
- #38, p. 664
- We use special components and the parallelogram rule to
write each vector in terms of a basis of vectors (equal
in number to the dimension of the space): for example, in
two-space, the usual basis is given by the two (perpendicular)
vectors denoted i and j:
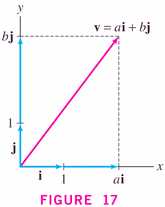
and, in three-space,
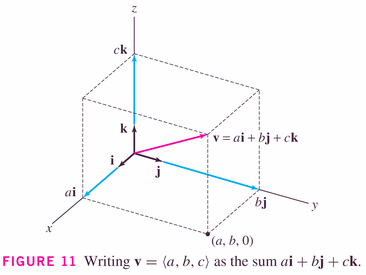
- Theorems:

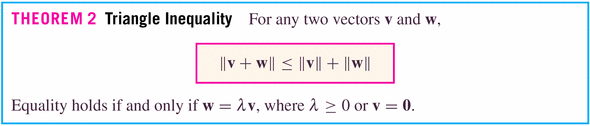
The Triangle inequality basically says that the diagonal of a parallelogram is shorter than or equal to the sum of the two sides:
"The shortest distance between two points is a straight line." In the case of Figure 17 (for vectors at right angles to each other)

and the only time you'll have equality is when either a or b is zero.
- #19, p. 664
- #29, p. 664
- #47, p. 664
- More physics:
- #58, p. 665
- #60, p. 665