- Homework 13.2 returned
- Grader: "Some people think that two vectors can point in the same direction een if they are not parallel!"
- Appeared to be a struggle on #45, p. 674.
- Sorry: your quizzes ended up at home; I'll have them on Thursday for you.
- Remember to look over the exam again, correcting your errors, and see me for 40% of your missed points back.
- Reminder: we'll have a review session Monday evening, prior to the final. This will be question and answer, 7:00-9:00, in this room (if we need to move, I'll post a sign). Let me know if you'll be coming late....
- There will be a quiz Thursday over the reading.
- Homework for section 13.3 is due Thursday (I'll post it on my door
Friday).
- It's time for course evaluations. Please take the time to visit eval.nku.edu, and give me your feedback. Thanks!
- We have looked at examples like #58, p. 665:
- First and foremost: Newton's laws of motion (in particular
), and statics.
- The parallelogram rule
- We can think of the force vectors on the cables as being composed of vector components (as well as coordinate components).
It turns out that we could see the solution very easily; calculating the force vectors was a little more complicated.
Now let's think a little more about how we resolve the vector forces into components: we'll find it convenient to define a product of two vectors as follows:

(how would you define this for vectors in two-space?). It's just component-wise multiplication, and we add up the results.
examples:
- #1, p. 680 (and let's practice drawing the line connecting the tips of these two position vectors)
- #6, p. 680
- #11, p. 681
It turns out that

where

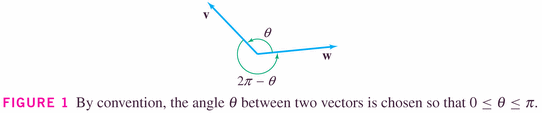


Otherwise, the angle is acute. examples:
- #23, p. 681
- Now: here's problem that really shows the power of this concept: #60, p. 681
Finally then, we can put it all together to get this:
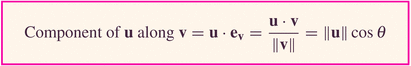
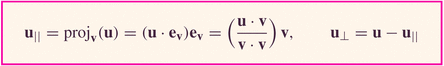
- First and foremost: Newton's laws of motion (in particular
- Additional examples:
- #53, 54, p. 681
- #70, p. 682 (bad picture -- looks like vector F can't make up its mind!)
- The next product we'll find convenient to define is the cross
product, which is a product of two vectors resulting in a third vector,
which juts into the space perpendicular to which the two vectors live.
It is only defined (and useful) in three-space, which makes it somewhat unusual (the dot product exists and is useful in any dimensional space).
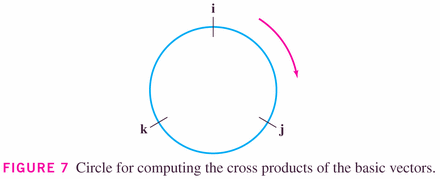
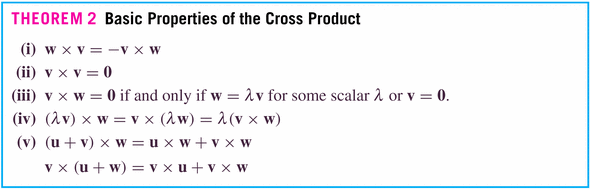
The cross product is linear in its components: that is,
This means that we can define it on the unit vectors in three space, and then deduce it using the component-wise definition of a three-vector.
- #20, p. 691
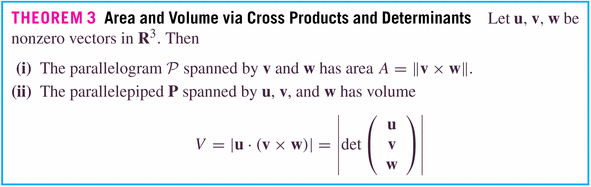
Now: here are the important geometric (rather than simply algebraic) properties of this product:

for the dot-product, it's the cosine; for the cross-product, it's the sine.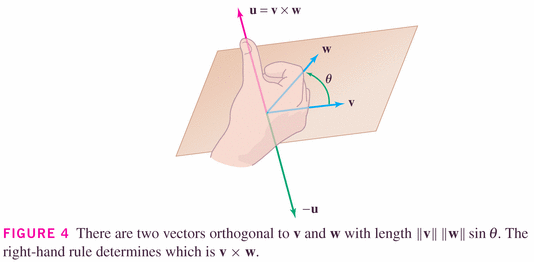
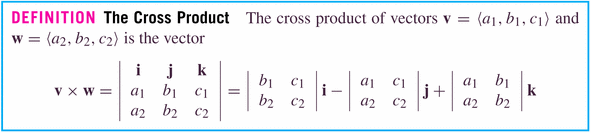
Example:
- #20, p. 691
Examples:
- #28, p. 691
- #46, p. 692
- The force
on a proton moving at velocity
(in m/s) in a uniform magnetic field
(in teslas) is
(in Newtons), where
Coulombs:
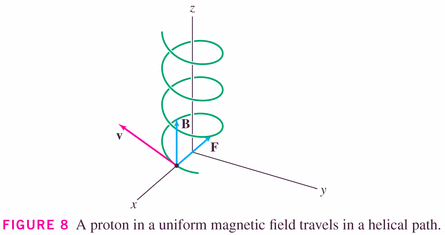
#36, p. 692
- Torque: #64, p. 693