Day 08: STA205 - Introduction to Statistical Methods

last time

next time

Today:

Announcements:
- Return of Quiz 4: Normals and Using the "Z-table"
- Return of Quiz 3: variation
  - mean: 7.8
  - sd: 2.5
  - median: 8.75
  - range: 8
  What does this tell you about the scores?
- Any questions over your homework problems?
Chapter 4, continued: Normally Distributed Data
- Z-statistic
  - The definition:
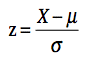
  - Using the Z-table backwards:
    - Strategy: see p. 130
    - Problem G of Chapter 4 Example
    - #5, p. 131
- Section 4.5: using the normal to make inferences
  - Someone makes a claim: does it make sense? How can we tell?
  - A common rule:
    If the probability of an observed sample is .05 or less (that is, a 1 in 20 chance of worse), assuming the truth of some conjecture, then the sample is contradictory to that conjecture. Otherwise the sample will not be considered contradictory to the conjecture.
  - Strategy: Inference making procedure, p. 136
  - Example: #3, p. 137
- Section 5.1: Sampling distributions and the normal curve (why is the normal distribution so important?)
  - A statistic is a number that we calculate from a sample of data: ${\bar{x},s^2,s}$
  - A parameter is a number that could be calculated from a population if all of the data were accessible: ${\mu,\sigma^2,\sigma}$
  - Generally we pull many values from a population to form a sample.
  - It turns out that if we take relatively large samples, sample after sample, and compute the statistic over and over, the histogram of statistic values will look bell-shaped.
  - The sampling distribution of the mean
  - Let's try that with coins: each of you will have a coin, and flip it 30 times. Our statistic will be the total number of heads.
  - Properties of the sampling distribution:
    - The mean of the sampling distribution of the sample mean ${\bar{x}}$ , denoted ${\mu_{\bar{x}}}$ , is equal to the mean of the population ${\mu}$ .
    - The standard deviation of the sampling distribution of the sample mean ${\bar{x}}$ , denoted ${\sigma_{\bar{x}}}$ , is
      
      ${\sigma_{\bar{x}}=\frac{\sigma}{\sqrt{n}}}$
      where n is the sample size. This statistic is called the standard error of the mean, and you will see it reported by StatCrunch, for example.
    - Here's the key thing: the sampling distribution is approximately normal for a large sample size n ("large" generally taken as $n\ge{30}$ ).
    - See Figure 5.5, p. 172
  - This result is encapsulated in The Central Limit Theorem (p. 167), and in the graphs of Figure 5.3, p. 168.
  - Calculating probabilities for sample means involves computing Z-scores, as we've done in the past: see p. 171.
  - Example problem: #4, p. 177
- Section 5.2: The Sampling distribution of the Sample Proportion
  - Definition: Consider a sample of qualitative data for which one category, or attribute, is of interest. To describe such a sample, we will use the proportion of the sample having the attribute of interest. This statistic is denoted by the letter p.
  - Properties of the sampling distribution of the sample proportion:
    - The mean of the sampling distribution of p, denoted , is equal to the mean of the population .
    - The standard deviation of the sampling distribution of p, denoted , is where n is the sample size.
    - Here's the key thing: the sampling distribution for p is approximately normal for a large sample size n ("large" generally taken as greater than or equal to n=30 at the very least, but in this case it depends as well on the value of ) as well.
    - Our choice of n to ensure normality is made so that three standard errors from the estimated are completely contained inside the interval [0,1]: and
    - See p. 186 for the strategy
    - See Figure 5.7 and 5.8, p. 182-183
  - Calculating probabilities for p involves computing Z-scores, as usual
  - Exercise #8, p. 189
  - Exercise #5, p. 202
Links
- Scientific calculator

Website maintained by Andy Long. Comments appreciated.