Today:
- Announcements:
- Return of Quiz 6: More of Normals and Using the "Z-table"
- The first exam is this Thursday, 2/26.
- Our exam will cover everything through 5.1
- Any questions over your homework problems, or the exam?
- Section 5.1: Sampling distributions and the normal curve (why is the
normal distribution so important?)
- Here's the key thing: the sampling distribution is approximately normal for a large sample size n ("large" generally taken as
).
- See Figure 5.5, p. 172
- This result is encapsulated in The Central Limit Theorem
(p. 167), and in the graphs of Figure 5.3, p. 168.
- Another Example problem: #6, p. 178
- A couple of key points, for parts a and b:
- You can't assume that the underlying distribution of the amount of coffee in an individual cup is normal.
- All we know is its mean and standard deviation.
- We can assume that the distribution of the sample mean is normally distributed, because we have a sample of more than 30.
- We can deduce the parameters of the sampling distribution of the sample mean from the parameters of the underlying distribution of the amount of coffee in an individual cup.
- Then we carry out the problem using the usual Z-Table tricks.
- For part c, we should understand that, as
, the sampling distribution of the sample mean will
- become more and more normal (by the Central Limit Theorem), and
- become tighter and tighter and tighter about the mean (smaller variance), as indicated by the standard error of the mean:
It gets smaller and smaller and smaller.
- Section 5.2: The Sampling distribution of the Sample Proportion
- Definition: Consider a sample of qualitative data for which
one category, or attribute, is of interest. To describe such a sample, we will
use the proportion of the sample having the attribute of interest. This
statistic is denoted by the letter p.
- Properties of the sampling distribution of the sample proportion:
- The mean of the sampling distribution of p, denoted
, is equal to the mean of the population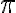 
- The standard deviation of the sampling distribution of p, denoted
, is
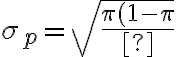}{n}}})
where n is the sample size.
- Here's the key thing: the sampling distribution for
p is approximately normal for a large sample size n ("large"
generally taken as greater than or equal to n=30 at the very
least, but in this case it depends as well on the value of
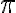) as well.
- Our choice of n to ensure normality is made so that
three standard errors from the estimated
are completely contained inside the interval [0,1]:
and
- See p. 186 for the strategy
- See Figure 5.7 and 5.8, p. 182-183
- Calculating probabilities for p involves computing
Z-scores, as usual
- Exercise #8, p. 189
- Using conjectured values of the population mean to make conjectures:
- check out p. 196 for strategy, first; then
- Exercise #5, p. 202
Links
Website maintained by Andy Long.
Comments appreciated.
Updated on 02/24/2009 16:39:47