- I will not be in at 9:00 tomorrow (I'll be in by 9:30).
- Quiz over Anova returned
- It's not enough to say "reject the null in favor of the alternative": what are the null and alternative?
- Reject the null (of no differences in means) before talking about differences.
- Quiz over
- This is your last quiz. There will be no quiz on Thursday.
- Note: Tutoring Workshops (review for final)
- Thu April 30: 2:30pm-4:30pm, SU108
- I'm planning a review on Monday night, 5/4. 7:00 pm-9:00
pm. It will really be a question-and-answer session, so come with your questions.
- It's time for course evaluations: those are to be done on-line. Please visit the site http://eval.nku.edu/ to do so.
You can carry this out until Friday of next week (May 1). Please participate!
- Statcrunch Portion of the final:
- At 3:00 today, I will post the "take home" portion of your final.
- You will be expected to analyze a small data set in several different ways.
- You will be asked to sign that you carried out the analysis entirely on your own.
- The results will be incorporated into your final exam, and constitute 25% of your exam. It is due with your final.
- The take-home component
- The web example from section 12.1 leads us into section 12.2. Once the
chi-square test indicates that there is dependence in the variables, we want to
have an easy way to describe it, and sample percentages is the easiest way.
- Note: we do not perform the chi-square test on the
percentages, but rather on the actual data collected instead. If we do not
detect a dependency, then we do not move to the discussion of the differences
in percentages.
- Back to the web example: example from website (use this data to reproduce the results in StatCrunch)
- Let's return to Exercise 1, page 503/509:
http://www.nku.edu/~statistics/data/c12s01e01.xls
- In contrast to chapter 12, where we attempted to determine if two
qualitative variables were dependent, in chapter 11 we look at the relationship
between two quantitative variables, and attempt to decide if it is
linear.
- We use a "scatterplot" to represent the two variables:
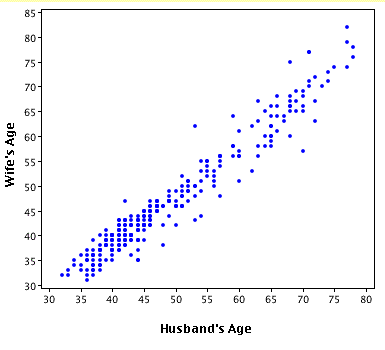
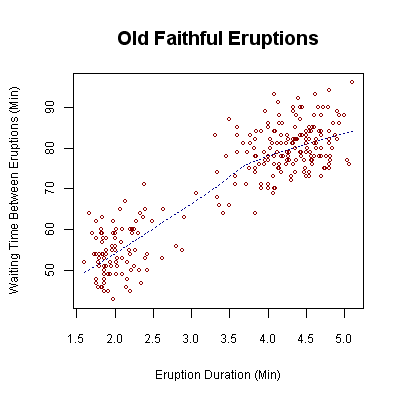
- Interpreting a scatterplot:
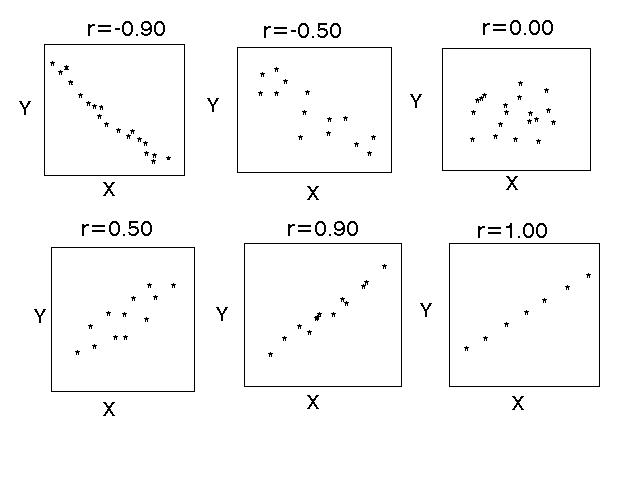
- positive linear relationship (as x increases, y increases)
- negative linear relationship (as x increases, y decreases)
- no linear relationship apparent
- Your conclusions should be drawn only for values of the independent variable (X) between the limits of the data values for X.
- Write your interpretation in terms of the variables of interest, not "X" and "Y"
- We use the correlation coefficient (denoted "r") to
characterize the strength of the linear relationship:
- See the image above!
- Always between -1 and 1
-
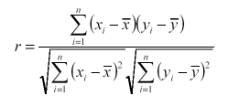
- correlation coefficient test: A test for linear dependence of two
variables (p. 446)
Decision rule: Accept Ha if
Test Statistic:
where n is the number of pairs, and df=n-2.
- Conditions for using the test for correlation (p. 447)
- At each value of x, the distribution of the y values in the population is normal, with standard deviation independent of x (see Figure 11.5, p. 447)
- The sampled values of y are independent of one another.
- Examples:
- Something too cool not to share: Gapminder
- STA205 on-line correlation and regression example (here's the data)
- Independent variables should give a "shotgun" appearance
to the scatterplot: example, two independent normal
variables.
- Let's look at the book example, Example 11.2, p. 437, in
StatCrunch:
http://www.nku.edu/~statistics/data/exam11-02.xls.
Is that relationship "not extremely strong"?
- Book exercise, #1, p. 444 and p. 451: http://www.nku.edu/~statistics/data/c11s01e01.xls
- Something too cool not to share: Gapminder