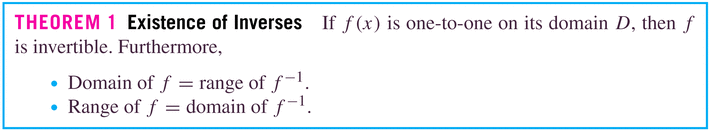Day 14 in MAT227

Last time: Section 7.1: exponential functions

Next time: Section 7.3: the natural log

Today:

Announcements:
- Notebooks returned today. Make sure that you put your name on your notebook!
  - I didn't actually assign a letter grade, but have communicated how I think that your notebook is looking. I'll only assign a letter grade at the end, and I'm looking for improvement! That is, I will be looking more at the later entries....
    Keep the postit note(s) I've attached with your journals, too.
  - Here's what I wrote, day 1:
    "The final 45 minutes [of class] is for discussion of new ideas. This will generally involve small group work as you work as a team to solve a problem. You will need a notebook (worth 5% of your grade) in which you will take notes on this process. For each entry you should have the following:
    1. Date
    2. Question
    3. Group member names
    4. Solution strategy or strategies proposed.
    5. Analysis of the process.
    We'll spend about 20 minutes on this phase. Then, for the final 25 minutes, we'll switch to a class discussion of the proposed solutions."
    What did I get? Not that! It seems that often it involved no actual English sentences, or coherent thoughts. It was just a few scratchings... Some specific problems:
    - No organization. Things include haphazardly.
    - Old homeworks included; NEW homeworks included!
    - Notes from class included (what have you done for the last two weeks?)
    - Notes from other classes included (what have you done for the last two weeks?)
  I want to add a requirement for each lab, and it's that you summarize the main point(s) of a lab. If you don't see the main points, then you should certainly ask! Can you go back over your labs and see the main point(s), the big idea(s)? You should be able to....
  Analysis and synthesis are the important buzz words. You're supposed to do some analysis, and that will lead to some synthesis (combining ideas perhaps already in your head).
  For example, I never once saw, on any lab, one of my synthetic rules: whenever you have two estimates, you have a third. This is an important rule, and something that I'd like you to remember - but if I don't write it up on the board, you don't write it down. Listen for those important synthetic rules, and come up with some of your own!
  An example of a synthetic rule which has made it down on several sheets is units are important. I've written it down, and that helps, but most of you didn't write it down: why not? Don't you agree?
- Homework Section 6.2 returned: 36 and 39 graded
- Homework Section 6.3 due today.
Last time we had a look at section 7.1: Derivative of and the number e.
- ${e^x}$ : "the great function of calculus", that only calculus could create.
- Amazing properties:
  1. ${e\approx{2.718281828459045}}$
    (irrational! the decimal representation doesn't repeat....)
  2. ${y=e^x}$ satisfies ${\frac{dy}{dx}=y}$
    (a differential equation, relating y and dy/dx)
  3. ${e^xe^X=e^{x+X}}$
    (One of the most important properties of the function ${e^x}$ )
  4. ${e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\ldots+\frac{x^n}{n!}+\ldots}$
    (this is called an infinite power series -- you can think of an exponential function as a sum of polynomial functions of higher and higher degree, going on forever! No wonder exponentials grow faster than any polynomial....)
  5. We can use the power series to write ${e=1+1+\frac{1}{2}+\frac{1}{3!}+\ldots+\frac{1}{n!}+\ldots}$ That's exactly what e is, and we can calculate e to any desired accuracy using it.
  6. I emphasized one thing in particular: the limit definition of the derivative, and the derivative of ${b^x}$ .
    ${\lim_{\Delta{x}\rightarrow{0}}\frac{b^{x+\Delta{x}}-b^{x}}{\Delta{x}}}=\lim_{\Delta{x}\rightarrow{0}}\frac{b^{x}b^{\Delta{x}}-b^{x}}{\Delta{x}}=b^{x}\lim_{\Delta{x}\rightarrow{0}}\frac{b^{\Delta{x}}-1}{\Delta{x}}=b^{x}\lim_{\Delta{x}\rightarrow{0}}\frac{b^{\Delta{x}}-b^0}{\Delta{x}}=b^{x}[b^x]'_{x=0}$
    Now, there's got to be one base ( ${b>0}$ ) such that the slope of the graph at 0 is exactly 1 -- and that base is e! That's the miracle....
What questions do you have about this topic, or any of our previous topics?
For today we're talking about inverse function, which requires that we start, perhaps, with "invertible functions".
- Here are some key properties and ideas:
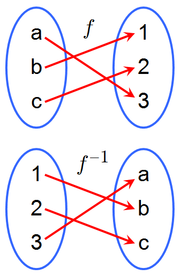
  - Here's the definition of the "undoing" property of inverse functions:
  - The crucial idea is the idea of being "one-to-one":
  - And here's the graphical test for "one-to-one-ness":
    So how will "one-to-one-ness" be reflected in the derivative? What property must the derivative of a continuous and differentiable function f have in order for the function f to be invertible?
  - As promised, this theorem asserts that the key property is one-to-one-ness. It also informs us about the difference between the two functions ${f\circ{f^{-1}}}$ and ${f^{-1}\circ{f}}$ :
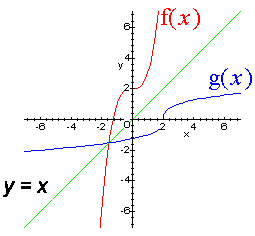
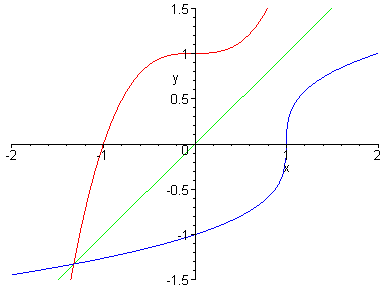
  - Graphical notes: the two functions ${f}$ and ${f^{-1}}$ are mirror reflections about the line y=x. It's easy to obtain the graph of an inverse, if you've got the graph of ${f}$ :
  - The derivative of an inverse function can be obtained by a trick, and it's one of those useful little things to see at some point in one's mathematical career:
    
    Proof: using the definition of the inverse, and the chain rule.
- Pick any examples you like (perhaps from the list below):
  - #8, p. 356
  - #9-16, p. 357
  - #20, p. 357
  - #22, p. 357
  - #31, p. 357
  - #33, p. 357
  - #42, p. 358
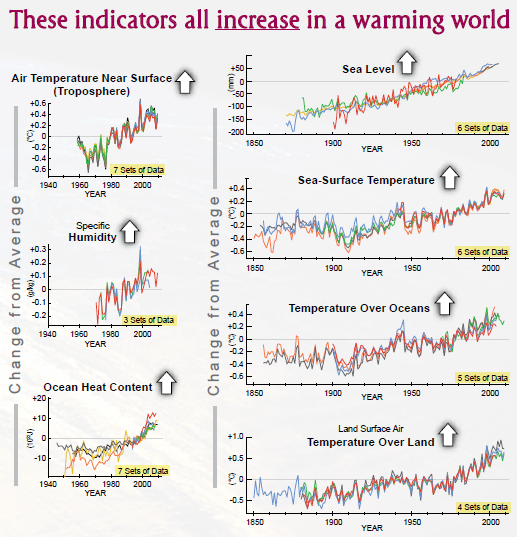
- Then we'll take a look at today's lab, which concerns some of our global data, and its invertibility.
- For the final 20 minutes, we'll switch to a class discussion of the proposed solution(s).
  1. What are we looking for in invertible functions?
  2. Do we expect to see invertibility in data?
  3. How about models?
  4. What's the mathematical focus in the following graphic?

Website maintained by Andy Long. Comments appreciated.