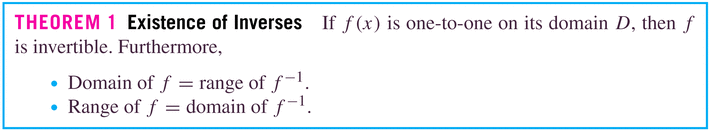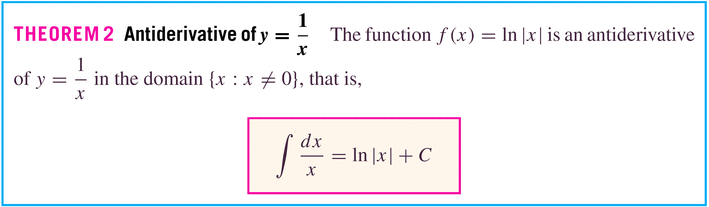Day 15 in MAT227

Today:

• Announcements:
  • Homework Section 6.3 returned: 4, 24, 36 graded
  • Homework Section 7.1 due today.

• Last time we had a look at section 7.2: inverse functions
  • Our aim is primarily the natural logarithm, the function that undoes the exponential function (although other inverses are also very important, e.g. arctan).

  • Here are some key properties and ideas:
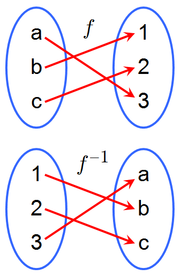
    • Here's the definition of the "undoing" property of inverse functions:

      

    • The crucial idea is the idea of being "one-to-one":

      

    • And here's the graphical test for "one-to-one-ness":

      

      So how will "one-to-one-ness" be reflected in the derivative? What property must the derivative of a continuous and differentiable function f have in order for the function f to be invertible?

    • As promised, this theorem asserts that the key property is one-to-one-ness. It also informs us about the difference between the two functions and :

      

    • Graphical notes: the two functions and are mirror reflections about the line y=x. It's easy to obtain the graph of an inverse, if you've got the graph of :

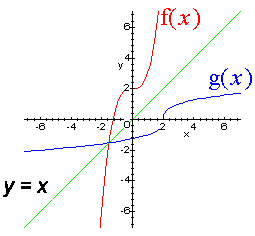
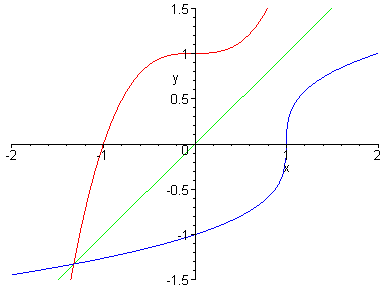
      We used this idea, and the graph of , to obtain the inverse of (the natural log, aka ).

    • The derivative of an inverse function can be obtained by a trick, and it's one of those useful little things to see at some point in one's mathematical career:

      

      Proof: using the definition of the inverse, and the chain rule.

    • From this we derived the derivative of the function :

  • Pick any examples you like (perhaps from the list below):
    • #8, p. 356
    • #9-16, p. 357
    • #20, p. 357
    • #22, p. 357
    • #31, p. 357
    • #33, p. 357
    • #42, p. 358

• Today: Section 7.3: logarithmic functions
  • Logs are, by definition, the inverses of the exponential functions:

    

  • The laws of logarithms are reflections (in the mirror along the line y=x) of the properties of exponentials:

    

    Most importantly,

    expoentials of sums are products, logs of products are sums.

    You should memorize all of these properties.

  • The derivation of the derivative of the natural log function is easy, given our work on inverses:

    

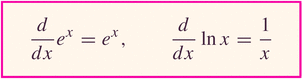
  • Another way to define the log function is as an anti-derivative of the "weird power" x^-1:

    

    Symmetry help us to understand the absolute value in this result: an antiderivative of the odd function 1/x is an even function ln(|x|).

  • More Examples:
    • 15-18, 20, p. 364
    • 45-50, p. 365, and draw!
    • 80, 84, 86, 90, 92, 94, p. 365
    • 108, p. 366
    • 109, p. 366

• Let's take a look at the inverse function lab, which concerns some of our global data, and the "invertibility of data and the models of data".

• As mentioned last time, if a variable transformed by logs appears linear, then the original variable was probably growing exponentially. This is the basis of lab15, concerning global temperatures.

• The lab is based on this analysis:

• For the final 20 minutes, we'll switch to a class discussion of the proposed solution(s).
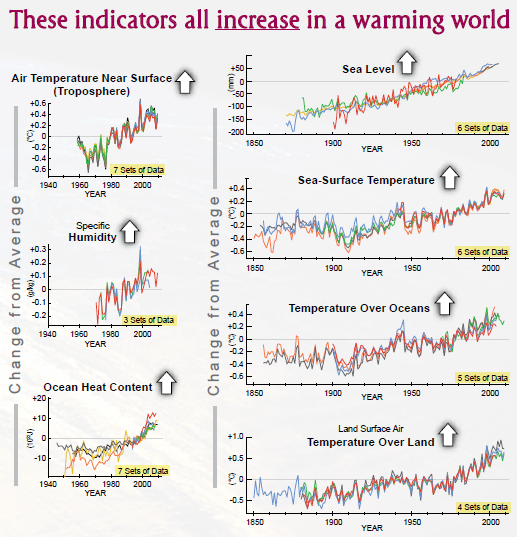
  1. What are we looking for in invertible functions?
  2. Do we expect to see invertibility in data?
  3. How about models?
  4. What's the mathematical focus in the following graphic?
  

• Here's an example of using logs to make a more complicated transformation (tricky but interesting example!):