- You have an assignment due
today, concerning bases.
- You have another assignment
due Monday, 10/10: make me a Fibonacci spiral.
- Make sure that you save your image somewhere where you can retrieve it if it doesn't get through to me the first time....
- Don't send me a link! It will no doubt be dead by the time I attempt to access it....
- New (reading) assignments (for Monday):
- Please read Pascal's Triangle, Idea #13, p. 52.
- To get an early start on our next topic, visit http://www.mathsisfun.com/platonic_solids.html to learn about the platonic solids.
- New homework assignment (for Friday, 10/14).
- Question of the day: What do Fibonacci numbers have to do
with Pascal's triangle?
-
The first few Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
144, ....
- We've seen that Fibonacci numbers occur in nature, in spirals.
- We build a Fibonacci spiral by attaching the largest square possible to rectangles, to create larger rectangles.
- The rectangles get closer and closer to golden
rectangles.
- Fibonacci Spiral Images
- I noticed some interesting ones....
- All of these, however, are fractals: that is, there's "the world within the world" in each. We'll talk more about Fractals before the end of the semester.
- We've seen that Fibonacci numbers occur in golden rectangles.
- The Greeks defined a golden rectangle by calling it the rectangle which, when the largest square possible is removed, retains its shape (which means that the ratio of side lengths doesn't change).
- The golden rectangle has side lengths in the ratio
Note that the value is only approximately 1.618:
is an irrational number, like
, and its decimal representation goes on forever and never repeats:
- Other rectangles....
- Now: what kind of rectangle will you get if you repeat the
Fibonacci spiral process with another kind of rectangle to
start (rather than a square)?
Turns out, that if you do it over and over and over again, you'll get a rectangle that gets more and more golden.
Let's try: we'll use a piece of grid paper (looking short and squat), and a 3x1 rectangle (start it running the tall-way at the 12th row down, 8th cell over).
Now, let's figure out what the recurrence relation is for the dimensions of our rectangles, and then figure out if we're getting golden....
- The A0
Paper Fractal
"A paper" is something you've no doubt encountered before: it's the long sheets we occasionly use (usually "A4" paper), which is far more common in Europe.
"A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.
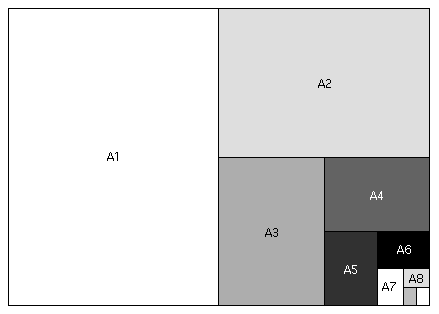
Let's see what the dimensions of A paper must be so that this requirement is fulfilled....
Call the long dimension of the A1 paper above
, and the short dimension 1.
- Then what are the dimensions of the A2 paper, according to the design of A paper?
- What is the value of
?
- Why not an A0 paper spiral? Let's try that....
This is the spiral, created using non-squares each time:
In both cases there's "the world within the world". Both are fractals.
- Now: what kind of rectangle will you get if you repeat the
Fibonacci spiral process with another kind of rectangle to
start (rather than a square)?
- One more place to look for Fibonacci numbers: in Pascal's Triangle (Idea #13, p. 52)
- This triangle is much older than Blaise
Pascal, who lived in the 17th century (it dates at least to
China, long before -- 13th century AD -- so at about the same
time as Fibonacci was doing his thing in Italy....)


One thing this allows us to do is to understand how this culture wrote its numbers (Chinese Bamboo Counting Rods). How did the Chinese of the 13th century write 15? 28? 30?
- The other Pascal's Triangle:


- How is it constructed? Easy!

- What's it good for?
- Pascal was interested in gambling -- that's why he studied it so hard.
- How many ways can you put 7 people into 2 cars to go to the party?
- Triangular numbers
- Tetrahedral numbers

- Where's Fibonacci?

- This triangle is much older than Blaise
Pascal, who lived in the 17th century (it dates at least to
China, long before -- 13th century AD -- so at about the same
time as Fibonacci was doing his thing in Italy....)
Links:
- More golden rectangle "applications"
- Fechner's experiments with the golden rectangle
- The golden ratio and aesthetics, by Mario Livio: "In spite of the Golden Ratio's truly amazing mathematical properties, and its propensity to pop up where least expected in natural phenomena, I believe that we should abandon its application as some sort of universal standard for "beauty," either in the human face or in the arts."
- An internet beauty contest of rectangles:
- the Museum of Harmony and Golden Section
- Fibonacci Numbers and the Golden Section
- The Cult of the Golden Ratio
- The Myth of the Golden Ratio