- Your Fibonacci spiral is due.
- Make sure that you save your image somewhere where you can retrieve it if it doesn't get through to me the first time....
- Don't send me a link! It will no doubt be dead by the time I attempt to access it....
- Fibonacci Spiral Images -- slight reprise
- Apologies: I haven't graded your homework from Friday yet -- I'll have it for you on Wednesday.
- You do have a homework
assignment (for Friday, 10/14).
- You have a new reading assignment: visit http://www.mathsisfun.com/platonic_solids.html to learn about the platonic solids.
- Reminder: you will have an exam after fall break, Friday the 21st.
- Question of the day: What makes some solids so Platonic?
- One more place to look for Fibonacci numbers: in Pascal's Triangle (Idea #13, p. 52)
- This triangle is much older than Blaise
Pascal, who lived in the 17th century (it dates at least to
China, long before -- 13th century AD -- so at about the same
time as Fibonacci was doing his thing in Italy....)

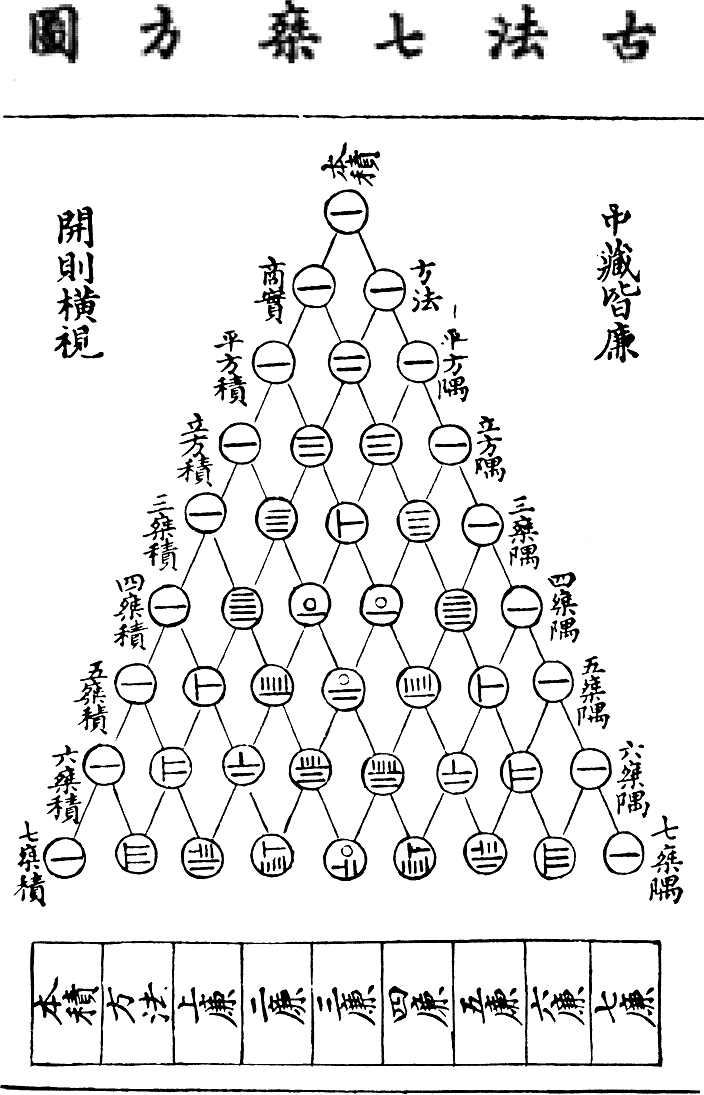
One thing this allows us to do is to understand how this culture wrote its numbers (Chinese Bamboo Counting Rods). How did the Chinese of the 13th century write 15? 28? 30?
With a partner: write the next line of the triangle, in Chinese counting rods.
- The other Pascal's Triangle:


- How is it constructed? Easy!

- What's it good for?
- Pascal was interested in gambling -- that's why he studied it so hard.
- How many ways can you put 7 people into 2 cars to go to the party?
- Triangular numbers
- Tetrahedral numbers

- Where's Fibonacci?

You might ask yourself: what is Fibonacci doing in there? Why that relationship?
- This triangle is much older than Blaise
Pascal, who lived in the 17th century (it dates at least to
China, long before -- 13th century AD -- so at about the same
time as Fibonacci was doing his thing in Italy....)
- Today's new topic: Platonic solids
- We begin our discussion with the convex regular
polygons:
"A regular polygon is a polygon which is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be convex or star."
- As an example, let's consider some regular convex hexagonal
graph paper, which represents a tiling of the plane by a
regular convex polygon.
- Now, let's move on to solids. A cube is an example of a Platonic
solid. It's the one we're most familiar with. The special thing about a
Platonic solid is that
- Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively), and
- All faces are congruent (identical) convex regular polygons.
- We'll start by trying to make some, using some kits. How many
Platonic solids are there, do you suppose?
- What's wrong with six sides, and beyond?
- Johannes Kepler thought that the orbits of the planets (of which
five were known at the time) were somehow related to the various
Platonic solids, as shown in this
figure.
"The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids."
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Dodecahedron Icosahedron 



- Now let's make a set of Platonic solids in 3-d: We're going to be
using two different methods to construct them:
- "geomags" and
- Platonic solids in 2-D (paper template)
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron Cube Octahedron Dodecahedron Icosahedron What conclusions can we draw from this data? Is there a pattern?
- We begin our discussion with the convex regular
polygons: