- Your quiz opportunity is over section 6.8 -- L'Hopital's rule.
- Your assignment over 6.4 will be due next time (Monday)
- Your assignment over 6.3 is returned:
- 14 -- Tamra
- 56 -- Sam
- I found some study materials from our textbook's author, and have made a sample available on-line. You might try the chapter 6 materials.
- Let's look at a few more problems involving these curious inverse
functions:
- 6, p. 459
- 14
- 22
- 67
- 49 -- there's always a ladder somewhere in calculus....
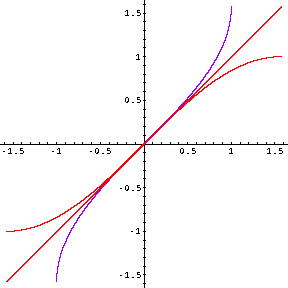
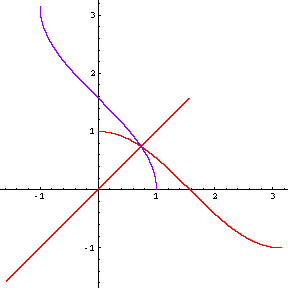
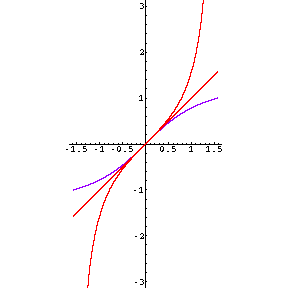
One thing that we notice about the inverses of sine and cosine is that one is simply a reflection and shift of the other (see exercise #18, p. 460).
- In financial mathematics we tend to use an unusual base for an
exponential:
- You may have encountered a few laws such as The rule of 72 (70, 71,
69.3,...) to calculate doubling time: forget them! Just do the
math: the question is
For what value of t is ?
Solving t is
for t, we get
where n is the number of compoundings per year, and r is given as a decimal (e.g. 9% is represented by .09). This is the doubling time.
When compounding is continuous (i.e.
), this reduces to the very lovely rule
- Now, how do we know that
?
?
The answer, of course, is L'Hopital's Rule, which is useful in solving certain indeterminate limits:

Let's rewrite it a little: we want to show that
- Here's the general situation:

- And if the limit of the quotient of the derivatives is
indeterminate, then iterate -- that is, do it again! Then work with the
ratio of the second (or higher) derivatives.
- Motivation of L'Hopital's Rule (requires the limit definition
of the derivative -- p. 471)
- Examples:
- Demonstration that
where
)
- Let's do a bunch of odds, #7-33, p. 477
- #70, p. 478
- #86, p. 478
- #93, p. 479
- Demonstration that