- You have a homework due today.
- Your quiz opportunity today is over 11.3: The Integral Test
- Our handout had one oother problem on it concerning series: related to Zeno.
- Here's how we make sense of an infinite sum today (don't know what Zeno would have thought):
- From the sequence
we define a new sequence
:
These are called partial sums. Notice that there are two indices running around, and that the limit refers to the summation's upper limit, not to the index of the sequence.
If
Then we say that
exists, and is equal to
. This justifies our probability distributions of the form
:
- Examples:
- #1, p. 735
- #4
- #15
- #17
- #10
- #47
- #87
- Other fractals (e.g. Koch snowflake)
- Beautiful spiral "proofs" of some infinite series
- From the sequence
- concerns several different means of testing for convergence of
series with all positive terms (obviously, if we're dealing with series
of all negative terms, similar results are going to apply).
- We're not so concerned with the actual limits (that is the values
of the series) as we are with the convergence (or divergence) of the
series.
- Theorems:

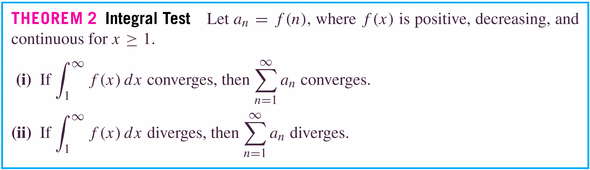
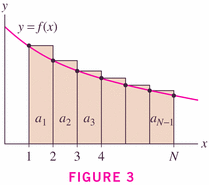
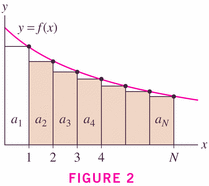
Theorem 3 is just a corollary of Theorem 2, where the integrals are the obvious power functions:

Let
, where f is a positive, decreasing function. If
converges by the integral test, and we define the remainder by
, then
(this gives us a bound on the error we're making in the calculation of a series). This is useful, for example, in the calculation of digits of
(now, you might ask "and what's the use of that?!";).
- Examples:
- Let's use this method to demonstrate conclusively that the harmonic series is non-convergent.
- Dominoes (here's my page) -- and here's a more elegant page in Mathematica: Divergence of the harmonic series (and dominoes!)