Day 53 in MAT229

Last time

Next time

Today:

Announcements:
- Return of your homework 12.2:
  - 2
  - 22
  - 26
- Quiz Opportunity today is over section 12.5
- Homework 12.3 is due today -- the last section covered for our last midterm exam on Thursday: it will cover everything from 11.8-11.11, and 12.1-12.3.
Section 12.5: Equations of Lines and Planes
- We'll approach this via a worksheet on lines and planes.
- Parametric Equations of Lines:
- Application of the Cross-Product: Equations of Planes
  - We'll start with planes through the origin: general planes are just displaced versions of these.
    Thus, the vectors I discuss in the next few lines can be considered position vectors, originating from the origin.
  - The parallelpiped equation
    
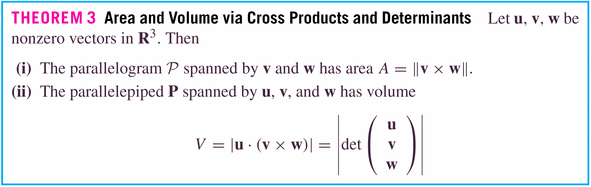
    gives us a hint as to how to write the equation of a plane containing ("spanned by") two vectors ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ : We want to find all vectors ${\underline{\bf{u}}}$ living in the space. Those will be the ones such that
    
    ${\underline{\bf{u}}\cdot(\underline{\bf{v}}\times\underline{\bf{w}})=0}$
    I.e., ${\underline{\bf{u}}}$ creates a zero volume parallelpiped, because it's living in the plane of ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ .
    This gives us our first equation of a plane: if the coordinates of ${\underline{\bf{u}}}$ are given by ${\langle{x,y,z}\rangle}$ and the coordinates of ${\underline{\bf{v}}\times\underline{\bf{w}}}$ are given by ${\langle{a,b,c}\rangle}$ (that is ${\langle{a,b,c}\rangle}$ is a normal vector) then the equation becomes
    
    ${ax+by+cz=0}$
    This is one form of the equation of a plane (through the origin). We say that the cross product ${\langle{a,b,c}\rangle}$ is normal to the vectors that live in the plane (or normal to the plane): that is, that it is perpendicular to the plane.
    Notice that we can instantly see a normal vector to the vectors in the plane in this form: just pick off the coefficients of the variables (a, b, and c) and turn those into a normal vector.
    
    Now (for the second equation!): notice that ${\underline{\bf{u}}=s\underline{\bf{v}}+t\underline{\bf{w}}}$ satisfies the equation of the plane ${\underline{\bf{u}}\cdot(\underline{\bf{v}}\times\underline{\bf{w}})=0}$ , since ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ are both perpendicular to their cross product. Hence we have another (parametric) equation of a plane (through the origin):
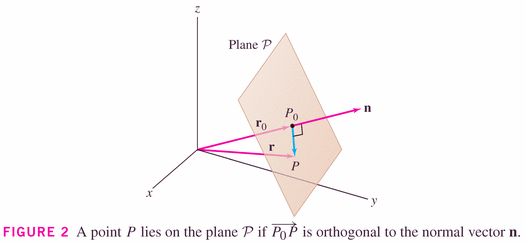
    ${\underline{\bf{u}}(s,t)=s\underline{\bf{v}}+t\underline{\bf{w}}}$
  - To offset these planes from the origin, one needs only reinterpret in the two forms of the equation:
    1. ${\underline{\bf{u}}=\underline{\bf{r}}-\underline{\bf{r}}_0=\langle{x,y,z}\rangle-\underline{\bf{r}}_0}$
      which leads to
      
      ${(\langle{x,y,z}\rangle-\underline{\bf{r}}_0)\cdot\langle{a,b,c}\rangle=0}$ or ${ax+by+cz=d}$
      where ${d=\underline{\bf{r}}_0\cdot\langle{a,b,c}\rangle}$
    2. ${\underline{\bf{u}}=s\underline{\bf{v}}+t\underline{\bf{w}}+\underline{\bf{r}}_0}$
      which leads to
      
      ${\underline{\bf{u}}(s,t)=s\underline{\bf{v}}+t\underline{\bf{w}}+\underline{\bf{r}}_0}$
  - Examples:
    - #3, p. 848
    - #13
    - #25
    - #61
Links
- Some nice calculus worksheets

Website maintained by Andy Long. Comments appreciated.