Day 54 in MAT229

Last time

Next time

Today:

Announcements:
- Return of your quiz
- Return of your homework 12.3:
  - 20 ("to the nearest degree")
  - 30 (Chad)
  - 64 (much easier than you thought)
- Last midterm exam on Thursday: it will cover everything from 11.8-11.11, and 12.1-12.3.
Questions about the material to be covered on the exam?
Section 12.5: Equations of Lines and Planes
- We'll approach this via a worksheet on lines and planes.
- Parametric Equations of Lines:
- Application of the Cross-Product: Equations of Planes
  - We'll start with planes through the origin: general planes are just displaced versions of these.
    Thus, the vectors I discuss in the next few lines can be considered position vectors, originating from the origin.
  - The parallelpiped equation
    
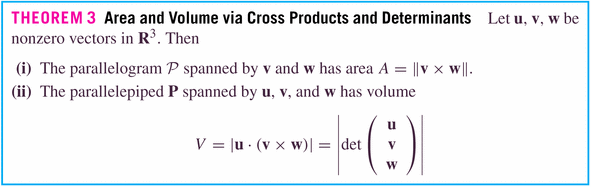
    gives us a hint as to how to write the equation of a plane containing ("spanned by") two vectors ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ : We want to find all vectors ${\underline{\bf{u}}}$ living in the space. Those will be the ones such that
    
    ${\underline{\bf{u}}\cdot(\underline{\bf{v}}\times\underline{\bf{w}})=0}$
    I.e., ${\underline{\bf{u}}}$ creates a zero volume parallelpiped, because it's living in the plane of ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ .
    This gives us our first equation of a plane: if the coordinates of ${\underline{\bf{u}}}$ are given by ${\langle{x,y,z}\rangle}$ and the coordinates of ${\underline{\bf{v}}\times\underline{\bf{w}}}$ are given by ${\langle{a,b,c}\rangle}$ (that is ${\langle{a,b,c}\rangle}$ is a normal vector) then the equation becomes
    
    ${ax+by+cz=0}$
    This is one form of the equation of a plane (through the origin). We say that the cross product ${\langle{a,b,c}\rangle}$ is normal to the vectors that live in the plane (or normal to the plane): that is, that it is perpendicular to the plane.
    Notice that we can instantly see a normal vector to the vectors in the plane in this form: just pick off the coefficients of the variables (a, b, and c) and turn those into a normal vector.
    
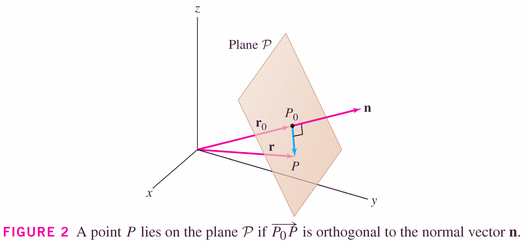
    Now (for the second equation!): notice that ${\underline{\bf{u}}=s\underline{\bf{v}}+t\underline{\bf{w}}}$ satisfies the equation of the plane ${\underline{\bf{u}}\cdot(\underline{\bf{v}}\times\underline{\bf{w}})=0}$ , since ${\underline{\bf{v}}}$ and ${\underline{\bf{w}}}$ are both perpendicular to their cross product. Hence we have another (parametric) equation of a plane (through the origin):
    ${\underline{\bf{u}}(s,t)=s\underline{\bf{v}}+t\underline{\bf{w}}}$
  - To offset these planes from the origin, one needs only reinterpret in the two forms of the equation:
    1. ${\underline{\bf{u}}=\underline{\bf{r}}-\underline{\bf{r}}_0=\langle{x,y,z}\rangle-\underline{\bf{r}}_0}$
      which leads to
      
      ${(\langle{x,y,z}\rangle-\underline{\bf{r}}_0)\cdot\langle{a,b,c}\rangle=0}$ or ${ax+by+cz=d}$
      where ${d=\underline{\bf{r}}_0\cdot\langle{a,b,c}\rangle}$
    2. ${\underline{\bf{u}}=s\underline{\bf{v}}+t\underline{\bf{w}}+\underline{\bf{r}}_0}$
      which leads to
      
      ${\underline{\bf{u}}(s,t)=s\underline{\bf{v}}+t\underline{\bf{w}}+\underline{\bf{r}}_0}$
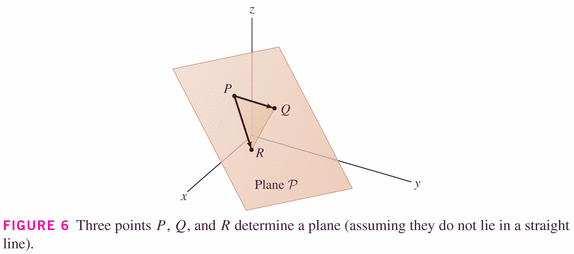
  - Examples:
    - #3, p. 848
    - #13
    - #25
    - #61

Section 10.1: Parametric Equations

And now for something completely different....

A good introduction to parametric curves is given by ballistics. If we shoot a bullet into the air with speed v horizontally, and we neglect all forces but gravity, then the bullet will trace out a parabola (some bullets are larger than others):

Now how might we characterize the path of the bullet? The answer is a parametric curve, of the form C(t)=(x(t), y(t)).

${x(t)=vt}$		${y(t)=h-\frac{1}{2}gt^2}$
or	${c(t)=(vt, h-\frac{1}{2}gt^2)}$
If we wish, we can solve for t in the equation for x and use that to eliminate the parameter t from the equation for y, hence getting an equation for the parabola traced out:
	${y=h-\frac{1}{2}g(\frac{x}{v})^2}$

Orbits of planets in the heavens, movements of ants on a hill, a robotic arm in an assembly plant: all these can be described by parametric curves.

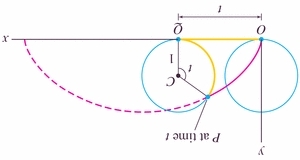
A couple of famous examples involving the cycloid:
- The Brachistochrone Problem (1696, solved by Newton in a single day after he heard the challenge)
- The Tautochrone Problem (1673)
Parametrizing a line:
Parametrizing a circle:
There are two distinctively different kinds of derivatives that we're going to have to consider here:
- There are the time-derivatives, which give us the actual speeds of the "particles" as they zip along in time. For the bullet, the speed will be
  
  ${s(t)=\sqrt{x'(t)^2+y'(t)^2}=\sqrt{v^2+(gt)^2}}$
- There is the slope of the tangent line to the curve traced out by the particle, which one can obtain using the time-derivatives:
  
  ${y'(x)=\frac{y'(t)}{x'(t)}=\frac{-gt}{v}=\frac{-gx}{v^2}}$
One of the most important applications of parametric curves is in the Bezier curve section. There are lots of important instances where we need to be able to design custom curves, and this is one of the most common ways of creating them. For example, you can use them to create your own "sigmac", using control points. (I had all my students create their own in numerical analysis.)
Examples:
- #, p.

Website maintained by Andy Long. Comments appreciated.
Updated on 04/18/2012 12:53:29