Day 4: Linear Algebra

• Your first assignment is due today.
• I'm hoping to demonstrate the freely available pdf viewer pdf-xchange today.

We had a look at the problem of characterizing the solution of a linear system, particularly when there are infinitely many solutions.
• We had definitions of free variables, matrices, vectors, and some operations on those vectors.
• Then we characterized a linear system as a matrix/vector problem, eliminating the need for the the variable names.
• Now, r.e. the solution when there are infinitely many solutions:
  • If we have just one equation, such as then we obviously have an infinite number of solutions. The solution, written as an ordered pair, is

    Notice

    1. that we have eliminated x;
    2. that we have written the solution entirely in terms of y, which is free (to take any real value we'd like);
    3. that x was a leading variable in the echelon form, but was eliminated via back-substitution of y.

    Finally we write that in a little different way: as vectors.

  • That equation came out of the more general system from our text: 2.7 Example, p. 14.

    Notice

    1. the advantage of the augmented matrix notation: it's so much cleaner. It eliminates what is non-essential (the choice of variable names). We realize that we're solving for three variables, but we are free to give them the names we choose.
    2. that the solution is given (p. 15) as a sum of vectors, some scaled by free variables ("scalar multiples").

• Let's check to make sure that everyone's okay with this vector/matrix formulation of things:
  1. 2.15, p. 18
  2. 2.18b,d
  3. 2.19 (pick one)
  4. 2.20
• Section One.I.3: General = Particular + Homogeneous
  • Definitions in this section:
    • zero vector (whose components are all zero)
    • homogeneous linear equation (has constant term 0)
    • homogeneous linear system (whose right hand side can be thought of as a zero vector in the augmented matrix)
    • particular solution: any solution of the original system
    • homogeneous solution: the complete solution of the homogeneous system
    • singular and non-singular matrices

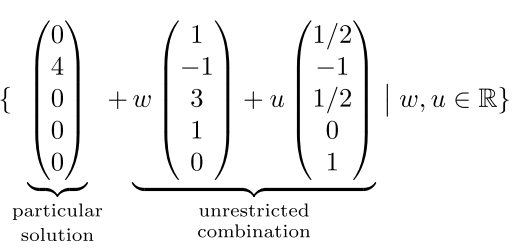
  • The upshot of the section is this: the general solution of a linear system (provided it exists) is a combination of one particular solution to the system itself, and the general solution to the homogeneous system:
    

  • This section features some proofs: our first examples of proofs (including one by induction). One of the activities that we're going to be doing in this course is actually proving theorems (or lemmas, which are theorems one encounters along the way to the proof of a theorem).

    In addition, we see a corollary (which is a theorem that follows directly, once a theorem has been proven).

  • From a general system we want to create two types of solutions:
    1. A particular solution, which is an actual solution of the given system; and
    2. a homogeneous solution, which is the general solution to an associated linear system (in which the RHS -- right-hand side -- is replaced with the zero vector).

    Let's consider an example -- the matrix system of example 2.7, which we considered earlier. Let's see how the solution can be written as a sum of these two kinds of vector solutions.

  • Our author points out (p. 22) one of the advantages of a homogeneous system: it always has at least one solution (since the zero vector is a solution).

    Let's take a look at page 22, for examples with unique versus infinitely many solutions.

Links: