- Your first assignment is returned today: graded
- 17 --
I like to see you making the row operations explicit.
That being said, I liked how some of you used "advanced methods" (i.e. augmented matrices) to solve these -- you're getting a little ahead of the section, but it allows you to practice a new technique against an old method.
Alignment is important: make your intermediate systems line up (in the variables).
Check your work using the answer pdf.
- 19 --
Do we have two solutions?
Because we had three equations in three unknowns, it was quite likely that we would have an inconsistent system -- which is what happened. Geometrically, what is the interpretation of the search for a solution?
- 34 -- we'd started this one in class, and even had
the particular solution. It's good to check each case
yourself, instead of simply saying "no other
solutions". There aren't that many possibilities, since
the number of coins is only 13....
You must justify your answers! The linear system has an infinite number of solutions, only one of which is practically possible.
- 17 --
- Your second assignment is due today.
- Definitions in this section:
- zero vector (whose components are all zero)
- homogeneous linear equation (has constant term 0)
- homogeneous linear system (whose right hand side can be thought of as a zero vector in the augmented matrix)
- particular solution: any solution of the original system
- homogeneous solution: the complete solution of the homogeneous system
- a generating or spanning set of vectors
- singular and non-singular matrices
As in section One.I.2, we're essentially reformulating the solution. We know how to solve for a solution of a linear system (if there is one); it's more a matter of how we represent it, or how we think of it.
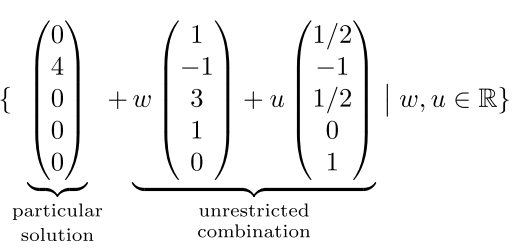
- The upshot of the section is this: the general solution of a
linear system (provided it exists) is a combination of any one
particular solution to the system itself, and the general solution to
the homogeneous system:
- This section features some proofs: our first examples of proofs
(including one by induction). One of the activities that we're going to
be doing in this course is actually proving theorems (or lemmas, which
are theorems one encounters along the way to the proof of a theorem).
In addition, we encounter a corollary (which is a theorem that follows directly, once a theorem has been proven).
- From a general system we attempt to derive two types of solutions:
- A particular solution, which is an actual solution -- with fixed values -- of the given system; and
- a homogeneous solution, which is the general solution to an associated linear system (in which the RHS -- right-hand side -- is replaced with the zero vector).
Let's consider an example -- the matrix system of example 2.7, which we considered earlier. Let's see how the solution can be written as a sum of these two kinds of vector solutions.
- Our author points out (p. 22) one of the advantages of a
homogeneous system: it always has at least one solution (since the zero
vector is a solution).
Let's take a look at page 22, for examples with unique versus infinitely many solutions.
- Now let's balance our own chemical equation (source):
"In order to write a correct chemical reaction, we must balance all of the atoms
on the left side of the reaction with the atoms on the right side. Let's look
at another example. Natural gas is primarily methane. Methane (CH4) is a
molecule in which 4 hydrogen atoms are bonded to one carbon atom. If you have
a gas stove, lighting the stove causes the methane to react with oxygen in the
atmosphere to release heat and the atoms recombine to form carbon dioxide and
water vapor.":
xCH4 + yO2 = zCO2 + wH2O This gives rise to a homogeneous system (one of whose solutions is "zeros all around" -- or, as we'll say, the zero vector.
- Let's try some problems:
- 3.15c, p. 29.
- 3.17
- 3.20abc
- 3.21ab