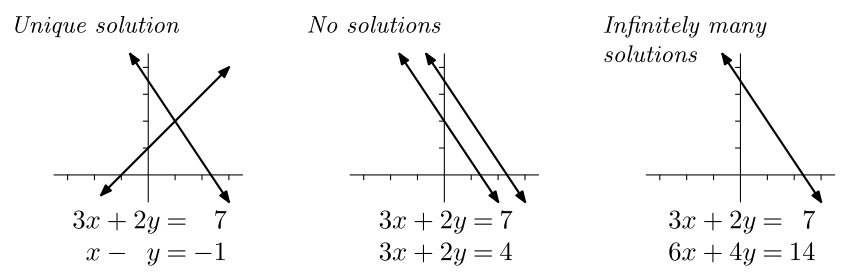- Your second assignment is returned today: graded
- 18ac -- please continue to show work. A step-by-step approach is really good here in the early going (in the end software will solve our big hard problems, of course).
- 27 -- use braces, and function notation in the end (although it did my soul good to see you using vectors to solve for the coefficients).
- 29 -- Be more daring! Your solutions were often
the authors with a change in variable name, or exchange
of rows, etc. Think about what each case means....
- 18ac -- please continue to show work. A step-by-step approach is really good here in the early going (in the end software will solve our big hard problems, of course).
- Some of you are making it easy on me by not submitting homework. It makes it easier on me, but it will make it harder on you. Be smart: do your homework.
- 3.15c, p. 29.
- 3.17
- 3.20abc
- 3.21ab
- To use the terminology of the previous section, we would characterize these three distinctly different systems of equations as follows:
- The first system has a particular solution vector, and the homogeneous system has only the unique solution of the zero vector;
- System two has a homogeneous soln with an infinite number of solutions, but no particular solution; and
- System three has a particular solution (e.g. (x,y)=(1,2), but the homogeneous solution has an infinite number of solutions.
- Definitions in this section:
- geometric vector (has length -- "magnitude" -- and direction)
- free vector: one which has no absolute location ("anchor") in space
- canonical (natural, standard) position: when a vector is anchored at the origin.
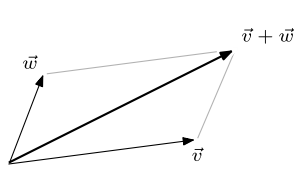
- parallelogram rule
- vector equation of a line (direction vector, position vector)

- k-dimensional linear surface
- hyperplane: a surface of dimension one fewer than the space itself.

Let's think about other ways to characterize this plane, perhaps some from your own experience.
- "We finish this subsection by restating our conclusions from the
first section in geometric terms. First, the solution set of a linear
system with n unknowns is a linear surface in
. Specifically, it is a k-dimensional linear surface, where k is the number of free variables in an echelon form version of the system. Second, the solution set of a homogeneous linear system is a linear surface passing through the origin. Finally, we can view the general solution set of any linear system as being the solution set of its associated homogeneous system ofset from the origin by a vector, namely by any particular solution."
- Let's try some problems:
- 1.1ac
- 1.3
- 1.6
Once again we're essentially reformulating the solution of a linear system, only this time geometrically. The picture is this (p. 32):