- Homework graded:
- 1.10, p. 164
- 1.13bc
- 1.30
- Your first project is due this coming Wednesday. Questions?
- Reminder: your next homework assignment is due Monday, 3/19 (special "hurry-up
due date"):
- 2.8, p. 172
- 2.9
- 2.11
- 2.22
- 1.19, p. 179
- 1.20
- 1.23
- 1.25
- 1.27
- You have a new homework assignment due Friday. Hence you have
something due every day next week. Ayeeeee!
-
Maps Between Spaces.Homomorphisms.Rangespace and Nullspace - Overview:
In this section we discover that a homomorphism
induces ("generates") two special subspaces: one in the domain space, V, and one in the "codomain" space W.
The important new space generated in the domain is the space of vectors that get mapped to the zero vector of space W (vectors that are "annihilated" by the homomorphism -- that sounds pretty exciting!).
The important new space generated in the codomain W is the space of vectors that are images of vectors of space V.
- Definitions:
- rangespace: The rangespace of a homomorphism
is
sometimes denoted
. The dimension of the rangespace is the map's rank. (See example 2.5, p. 183.)
- nullspace: The nullspace (or
kernel) of a linear map
is the inverse image of
:
. The dimension of the nullspace is the map's nullity.
- nonsingular: A linear map that is one-to-one is nonsingular.
- rangespace: The rangespace of a homomorphism
- Theorems:
- 2.1 Lemma: Under a homomorphism, the image of any
subspace of the domain is a subspace of the
codomain. In particular, the image of the entire domain
space, which is the range of the homomorphism, is a
subspace of the codomain. [Hence a homomorphism
generates lots of subspace!]
- 2.14 Theorem: A linear map's rank plus its nullity
equals the dimension of its domain vector space
V. [Everything goes somewhere, essentially.]
- 2.17 Corollary: The rank of a linear map is less
than or equal to the dimension of the domain. Equality
holds if and only if the nullity of the map is
zero. [In this case the map is one-to-one.]
- 2.18 Lemma: Under a linear map, the image of a
linearly dependent set is linearly dependent.
- 2.21 Theorem:

- 2.1 Lemma: Under a homomorphism, the image of any
subspace of the domain is a subspace of the
codomain. In particular, the image of the entire domain
space, which is the range of the homomorphism, is a
subspace of the codomain. [Hence a homomorphism
generates lots of subspace!]
- Examples:
- 2.22, p. 190
- 2.23
- 2.24 (let's also give example maps)
- Overview:
-
Maps Between Spaces.Computing Linear Maps.Representing Linear Maps with Matrices "...a linear map is determined by its action on a basis."
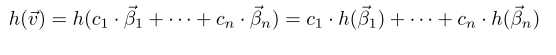
- Summary: A homomorphism is determined by its action on a basis. That
is, if
is a basis of a vector space V and
are (perhaps not distinct) elements of a vector space W, then there exists a homomorphism from V to W sending
to
, and that homomorphism is unique.
Let's take a good look at example 1.1 from this section, p. 193.
At the end of this example, bottom of p. 194, the author defines (essentially creates a) matrix multiplication. This definition is crucial for all that follows.
- Definitions:
- matrix representation of homomorphism h
with respect to B, D (bases of domain and
codomain, respectively:

-
matrix multiplication:

Observe the essential alignment of dimensions:
- the number of rows in the vector multiplied by the matrix must conform to the number of columns of the matrix.
- The number of rows of the result will conform to the number of rows of the matrix.
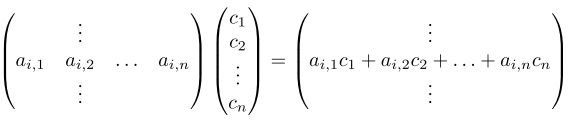
"Matrix-vector product can also be viewed column-by-column."
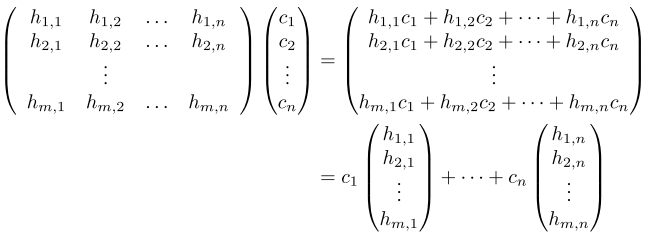
- matrix representation of homomorphism h
with respect to B, D (bases of domain and
codomain, respectively:
- Theorems:
- Theorem 1.4:

- Theorem 1.4:
- Examples:
- Really important example: 1.8, p. 198
- 1.11, p. 200 -- let's think of the multiplication in as many different ways as possible...
- 1.13 -- flashback to linear systems.
- Summary: A homomorphism is determined by its action on a basis. That
is, if