- Again: Important notice:
- The book has been updated (unbeknownst to me! Grrrr....).
- Hence problem numbers do not correspond to those I'm using.
- Until I hear back from the author about the extent of the changes, I'll continue to use the original copy that we used at the start of the semester.
- There are links to the original and the answers on our course webpage.
- You can still hand in your last homework (because of this confusion).
- Your first
project is due today. I've gotten several emailed to me, which is fine.
-
Maps Between Spaces.Computing Linear Maps.Representing Linear Maps with Matrices "...a linear map is determined by its action on a basis."
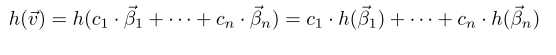
In this section we re-express homomorphisms as matrices.
- Summary: A homomorphism is determined by its action on a basis. That
is, if
is a basis of a vector space V and
are (perhaps not distinct) elements of a vector space W, then there exists a homomorphism from V to W sending
to
, and that homomorphism is unique.
Let's take a good look at example 1.1 from this section, p. 193.
At the end of this example, bottom of p. 194, the author defines (essentially creates a) matrix multiplication. This definition is crucial for all that follows.
- Definitions:
- matrix representation of homomorphism h
with respect to B, D (bases of domain and
codomain, respectively:

-
matrix multiplication:

Observe the essential alignment of dimensions:
- the number of rows in the vector multiplied by the matrix must conform to the number of columns of the matrix.
- The number of rows of the result will conform to the number of rows of the matrix.
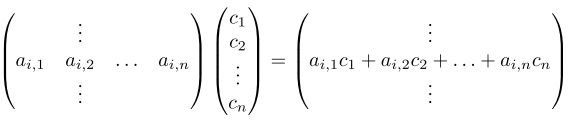
"Matrix-vector product can also be viewed column-by-column."
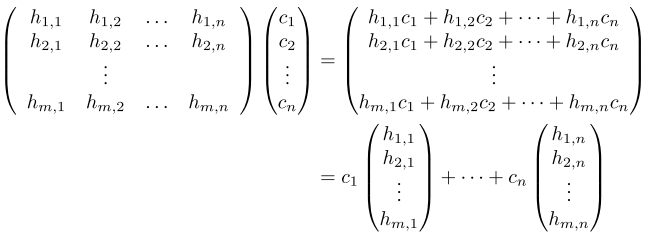
- matrix representation of homomorphism h
with respect to B, D (bases of domain and
codomain, respectively:
- Theorems:
- Theorem 1.4:

- Theorem 1.4:
- Examples:
- Really important example: 1.8, p. 198
- 1.11, p. 200 -- let's think of the multiplication in as many different ways as possible...
- 1.13 -- flashback to linear systems, to column
spaces, and now to thinking of matrix
multiplication as a linear map taking vectors
in one space to another space.
Remember: all finite dimensional vector spaces are essentially equivalent!
- Summary: A homomorphism is determined by its action on a basis. That
is, if
-
Maps Between Spaces.Computing Linear Maps.Any Matrix Represents a Linear Map - Summary: "The prior subsection shows that the action of a linear
map h is described by a matrix H, with respect to
appropriate bases.... In this subsection, we will show the
converse, that each matrix represents a linear map."
"....In practice, when we are working with a matrix but no spaces or bases have been specified, we will often take the domain and codomain to be
and
and use the standard bases."
- Definitions:
- Theorems:
- Theorem 2.1: Any matrix represents a homomorphism
between vector spaces of appropriate dimensions, with respect
to any pair of bases.
- Theorem 2.3: The rank of a matrix equals the rank
of any map that it represents.
- Corollary 2.5: Let h be a linear map
represented by a matrix H. Then h is onto if and
only if the rank of H equals the number of its rows, and
h is one-to-one if and only if the rank of H
equals the number of its columns.
- Corollary 2.6: A square matrix represents nonsingular maps if and only if it is a nonsingular matrix. Thus, a matrix represents an isomorphism if and only if it is square and nonsingular.
- Theorem 2.1: Any matrix represents a homomorphism
between vector spaces of appropriate dimensions, with respect
to any pair of bases.
- Examples:
- Let's look at a better example, perhaps, to motivate Example 2.2, p. 204.
- 2.10a, p. 207
- 2.11 -- notice that our author relates the mapping back to the standard basis. It's our preferred way of thinking about
- 2.12
- Summary: "The prior subsection shows that the action of a linear
map h is described by a matrix H, with respect to
appropriate bases.... In this subsection, we will show the
converse, that each matrix represents a linear map."