Day 31: Linear Algebra

Last Time

Next Time

Today:

Announcements:
- You have a homework due today.
- I won't be here Friday, but I've arranged for Prof. Mike Waters to come in Friday and go over an example which will illustrate how to carry out your second project. I think that this will be a very valuable class.
- You do have an exam coming up next week. It will be through the material we're working on today: inverses (III.IV.4).
We are considering "Matrix Operations":

Maps Between Spaces.Matrix Operations
of which there are four subsections:
1. Sums and Scalar Products
  - Occur in the obvious way.
  - Scalar multiple of a matrix -- multiply each component
  - Sum of matrices -- component-wise addition (the dimensions of the matrices must be the same!).
2. Matrix Multiplication
  - This is defined in the "obvious" way: by treating the second matrix in the product ${AB}$ as a bunch of columns, and doing each matrix multiplication on each column and pasting the results together:
    
    ${AB=(A\overline{b}_1\ A\overline{b}_2\ \cdots A\overline{b}_n)}$
  - Definitions:
  - Theorems:
    1. A composition of linear maps is linear.
    2. A composition of linear maps is represented by the matrix product of the representative matrices.
3. Mechanics of Multiplication
  - Definitions:
    1. A matrix with all zeroes except for a one in the ${a_{i,j}}$ entry is an i,j-unit matrix.
    2. The main diagonal (or principle diagonal or diagonal) of a square matrix goes from the upper left to the lower right, constituted of the entries ${a_{i,i}}$ .
    3. Zero Matrix: matrix whose entries are identically zero
    4. Diagonal Matrix: a square matrix whose only non-zero entries are found in the entries ${a_{i,i}}$
    5. Identity Matrix: a diagonal matrix whose diagonal entries are all 1: ${a_{i,i}=1}$
    6. A permutation matrix is square and is all zeros except for a single one in each row and column. (If you like, it's a "mixed-up" identity matrix, where the rows have been shuffled.)
    7. Reduction Matrices: There are three matrices which perform the operations of Gaussian elimination.
  - Theorems:
    1. Lemma: Gaussian reduction can be done through matrix multiplication:
    2. Corollary 3.22
      
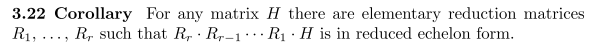
      (We simply apply the appropriate reduction matrices over and over....)
4. Inverses
  - These are the trickiest....
  - Last time we "figured out" how to invert the matrix
    
    ${H=\left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {1}&{1}&{0}&{0}\cr {1}&{1}&{1}&{0}\cr {1}&{1}&{1}&{1} \end{array} \right) }$
    getting the matrix
    
    ${H^{-1}=\left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {-1}&{1}&{0}&{0}\cr {0}&{-1}&{1}&{0}\cr {0}&{0}&{-1}&{1} \end{array} \right) }$
    and we verified that the product of these two matrices is the identity matrix.
  Let's find a more systematic way of obtaining the inverse. The secret is in thinking about row-reduction, and Gauss-Jordan reduction in particular.
  Gauss-Jordan reduction turns a matrix into the identity matrix (if possible). Since that is our goal, the question becomes how to turn Gauss-Jordan reduction into an inverse matrix?
  Since reduction is represented by three different types of matrix homomorphisms, we simply multiply the necessary set of instructions to turn a matrix into the identity matrix. Then the product of the reduction matrices will be the desired inverse.
  1. Let's look at our example from last time:
    We begin by successively replacing the rows below the first with the given row minus the first row: we read this from right to left -- so the first homomorphism replaces the second row, the second replaces the third row, and the third replaces the fourth row.
    
    ${ \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {-1}&{0}&{0}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {-1}&{0}&{1}&{0}\cr {0}&{0}&{0}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {-1}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {0}&{0}&{0}&{1} \end{array} \right) = \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {-1}&{1}&{0}&{0}\cr {-1}&{0}&{1}&{0}\cr {-1}&{0}&{0}&{1} \end{array} \right) }$
    
    Now we apply this to the given matrix:
    
    ${ \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {-1}&{1}&{0}&{0}\cr {-1}&{0}&{1}&{0}\cr {-1}&{0}&{0}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {1}&{1}&{0}&{0}\cr {1}&{1}&{1}&{0}\cr {1}&{1}&{1}&{1} \end{array} \right) = \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{1}&{1}&{0}\cr {0}&{1}&{1}&{1} \end{array} \right) }$
    
    Now we do it again, but leave the first and second rows alone:
    
    ${ \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{-1}&{1}&{0}\cr {0}&{-1}&{0}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{1}&{1}&{0}\cr {0}&{1}&{1}&{1} \end{array} \right) = \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {0}&{0}&{1}&{1} \end{array} \right) }$
    one more time, leaving all but the last alone:
    
    ${ \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {0}&{0}&{-1}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {0}&{0}&{1}&{1} \end{array} \right) = \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {0}&{0}&{0}&{1} \end{array} \right) }$
    
    Okay! so now let's put all these transformations together, to get the inverse::
    
    ${ \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{0}&{1}&{0}\cr {0}&{0}&{-1}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {0}&{1}&{0}&{0}\cr {0}&{-1}&{1}&{0}\cr {0}&{-1}&{0}&{1} \end{array} \right) \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {-1}&{1}&{0}&{0}\cr {-1}&{0}&{1}&{0}\cr {-1}&{0}&{0}&{1} \end{array} \right) = \left( \begin{array}{cccc} {1}&{0}&{0}&{0}\cr {-1}&{1}&{0}&{0}\cr {0}&{-1}&{1}&{0}\cr {0}&{0}&{-1}&{1} \end{array} \right) }$
    
    Before leaving this example, let's verify that, if ${HH^{-1}=I}$ , then ${H^{-1}H=I}$ .
    This will always be true for square matrices. However I want to emphasize that, in general, matrix multiplication is not commutative: that is, in general,
    ${AB\ne{BA}}$
    First of all, the dimensions may not work out; secondly, even if the dimensions do work (square matrices), then it may not work.
  2. Our author discusses right and left inverses in section III.IV.4. Let's take a look at his first example, on p. 229. What matrices are associated with these homomorphisms? Why left and right?
  3. Let's look at another example. We've seen homomorphisms associated with rotations and projections from into .
    Let's see how the mechanical issues of the four subsections come about.
    Let's continue to think about rotations of ${\R^2}$ onto ${\R^2}$ .
    What about compositions of rotations? A rotation, followed by another rotation, should also be a homomorphism. Let's use the standard bases, and represent each rotation as a matrix, then represent the composition. This leads to matrix multiplication. It also gives us a way of deriving two extremely important trigonometric identities!
    Now: how would we invert a rotation of say ${\theta}$ , in the counter-clockwise sense?
    How do we invert any isomorphism of ${\R^2}$ onto ${\R^2}$ ?
    What other kinds of homomorphisms can we think of, along the same lines? We've looked at two kinds of homomorphisms of ${\R^2}$ into ${\R^2}$ :
    1. rotations
    2. projections
    What other kinds of homomorphisms can you think of? And what if we combine (compose) these?

Website maintained by Andy Long. Comments appreciated.