- Homework graded:
- 2.26 -- shadows....
- 2.28 -- label axes: please do a decent job of graphing these lines!
- 2.29a,d -- need to show work.
- You have a homework due next time.
- I haven't graded the projects yet, but hope to have them graded by Friday.
-
Maps Between Spaces.Computing Linear Maps.Representing Linear Maps with Matrices "...a linear map is determined by its action on a basis."
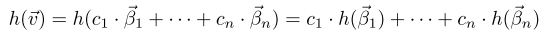
In this section we re-express homomorphisms as matrices.
- Summary: A homomorphism is determined by its action on a basis. That
is, if
is a basis of a vector space V and
are (perhaps not distinct) elements of a vector space W, then there exists a homomorphism from V to W sending
to
, and that homomorphism is unique.
Let's take a good look at example 1.1 from this section, p. 193.
At the end of this example, bottom of p. 194, the author defines (essentially creates a) matrix multiplication. This definition is crucial for all that follows.
- Definitions:
- matrix representation of homomorphism h
with respect to B, D (bases of domain and
codomain, respectively:

-
matrix multiplication:

Observe the essential alignment of dimensions:
- the number of rows in the vector multiplied by the matrix must conform to the number of columns of the matrix.
- The number of rows of the result will conform to the number of rows of the matrix.
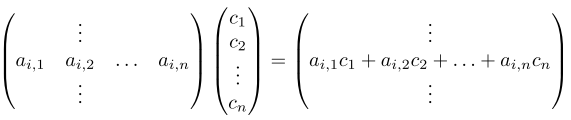
"Matrix-vector product can also be viewed column-by-column."
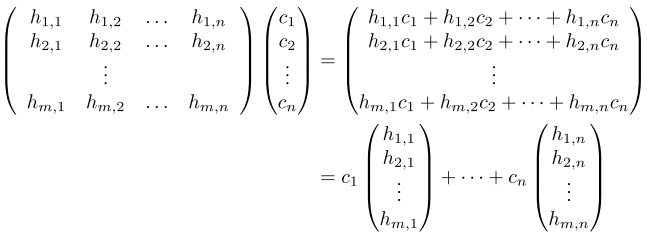
- matrix representation of homomorphism h
with respect to B, D (bases of domain and
codomain, respectively:
- Theorems:
- Theorem 1.4:

- Theorem 1.4:
- Examples:
- Really important example: 1.8, p. 198
- 1.11, p. 200 -- let's think of the multiplication in as many different ways as possible...
- 1.13 -- flashback to linear systems, to column
spaces, and now to thinking of matrix
multiplication as a linear map taking vectors
in one space to another space.
Remember: all finite dimensional vector spaces are essentially equivalent!
- Summary: A homomorphism is determined by its action on a basis. That
is, if
-
Maps Between Spaces.Computing Linear Maps.Any Matrix Represents a Linear Map - Summary: "The prior subsection shows that the action of a linear
map h is described by a matrix H, with respect to
appropriate bases.... In this subsection, we will show the
converse, that each matrix represents a linear map."
"....In practice, when we are working with a matrix but no spaces or bases have been specified, we will often take the domain and codomain to be
and
and use the standard bases."
- Definitions:
- Theorems:
- Theorem 2.1: Any matrix represents a homomorphism
between vector spaces of appropriate dimensions, with respect
to any pair of bases.
- Theorem 2.3: The rank of a matrix equals the rank
of any map that it represents.
- Corollary 2.5: Let h be a linear map
represented by a matrix H. Then h is onto if and
only if the rank of H equals the number of its rows, and
h is one-to-one if and only if the rank of H
equals the number of its columns.
- Corollary 2.6: A square matrix represents nonsingular maps if and only if it is a nonsingular matrix. Thus, a matrix represents an isomorphism if and only if it is square and nonsingular.
- Theorem 2.1: Any matrix represents a homomorphism
between vector spaces of appropriate dimensions, with respect
to any pair of bases.
- Examples:
- Let's look at a better example, perhaps, to motivate Example 2.2, p. 204.
- Example 2.2, p. 204 (reprise)
- 2.10a, p. 207
- 2.11 -- notice that our author relates the mapping back to the standard basis. It's our preferred way of thinking about
- 2.12
- Summary: "The prior subsection shows that the action of a linear
map h is described by a matrix H, with respect to
appropriate bases.... In this subsection, we will show the
converse, that each matrix represents a linear map."
There are four subsections:
- Sums and Scalar Products
- Occur in the obvious way.
- Scalar multiple of a matrix -- multiply each component
- Sum of matrices -- component-wise addition (the dimensions of the matrices must be the same!).
- Matrix Multiplication
- This is defined in the "obvious" way: by treating the second matrix in the product
as a bunch of columns, and doing each matrix multiplication on each column and pasting the results together:
- Definitions:
- Theorems:
- A composition of linear maps is linear.
- A composition of linear maps is represented by the matrix product of the representative matrices.
- This is defined in the "obvious" way: by treating the second matrix in the product
- Mechanics of Multiplication
- Definitions:
- A matrix with all zeroes except for a one in the
entry is an i,j-unit matrix.
- The main diagonal (or principle diagonal or
diagonal) of a
square matrix goes from the upper left to the
lower right, constituted of the entries
.
- Zero Matrix: matrix whose entries are identically zero
- Diagonal Matrix: a square matrix whose only non-zero entries are found in the entries
- Identity Matrix: a diagonal matrix whose diagonal entries are all 1:
- A permutation matrix is square and is all zeros except for a single one in each row and column. (If you like, it's a "mixed-up" identity matrix, where the rows have been shuffled.)
- Reduction Matrices: There are three matrices which perform the operations of Gaussian elimination.
- A matrix with all zeroes except for a one in the
- Theorems:
- Corollary 3.22
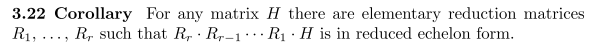
(We simply apply the appropriate reduction matrices over and over....)
- Corollary 3.22
- Definitions:
- Inverses
- These are the trickiest....
Let's see how the mechanical issues of the four subsections come about.
Let's continue to think about rotations of onto
.
What about compositions of rotations? A rotation, followed by another rotation, should also be a homomorphism. Let's use the standard bases, and represent each rotation as a matrix, then represent the composition. This leads to matrix multiplication. It also gives us a way of deriving two extremely important trigonometric identities!
Now: how would we invert a rotation of say , in the
counter-clockwise sense?
How do we invert any isomorphism of onto
?
What other kinds of homomorphisms can we think of, along the same lines? We've looked at two kinds of homomorphisms of into
:
- rotations
- projections