Day 14 in MAT229

Last time

Next time

Today:

Announcements:
- Homework 6.6 is returned.
  - 40, p. 460: make sure that you plot your result, to see if it's really tangent!
  - 64: u-substitution
  - 68: u-substitution
- Your test next week will be through 7.1.
- I've reserved computer lab 310 for this Friday, 9/12, at 9:00. So those who are able may join me as we go over some of the basics of Mathematica. I've also reserved it for a couple of more Fridays, the 26th of September and the 3rd of October.
Continuing with section 7.1: Integration by parts.
- First of all, the big picture: integration by parts is just the product rule backwards. This integration technique, like all integration techniques, is really just a differentiation technique in reverse.
  Consider the method of u-substitution, for example. That's just the chain rule in reverse.
- Derivation of the integration by parts formula:
  We start with the product rule:
  
  ${\left[u(x)v(x)\right]'=u(x)v'(x)+v(x)u'(x)}$
  Now integrate both sides:
  
  ${\int_{}^{}\left[u(x)v(x)\right]'dx=\int_{}^{}\left[{u(x)v'(x)+v(x)u'(x)}\right]dx}$
  
  ${\int_{}^{}u(x)v'(x)dx=u(x)v(x)-\int_{}^{}v(x)u'(x)dx}$
  
  ${\int_{}^{}udv=uv-\int_{}^{}vdu}$
- We'll motivate this technique by considering exercises #9 and #66, p. 492 in detail.
- Integration by parts may need to be carried out multiple times: sometimes the idea is to simplify the integral each time, until a really simple one arises allowing us to calculate the final solution (e.g. Example 6, p. 491). Sometimes it's something of a trick: we compute the integral multiple times in order to return to the original integral, allowing us to solve an equation for the original integral (e.g. Example 4, p. 490).
- Suggested strategy:
  - Choose u so that u' is simpler than u itself.
  - Choose v' so that $v=\int_{}^{}v'dx$ can be evaluated.
  - Sometimes v'=1 is a good choice.
- Of course, all this works with definite integrals:
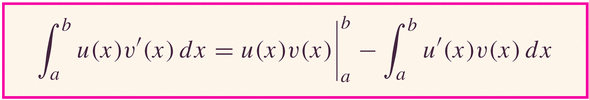
- Examples:
  1. #10, p. 492
  2. #26
  3. #39
  4. #40
  5. #51
section 7.2: Trigonometric Integrals
- We'll look at a few examples which illustrate the importance of trigonometric identities
  - #65, p. 501; this one prepares us for the two that follow.
  - #1
  - #6
- Now let's look at some of the useful identities that we'll want to use from time to time. The good news is that only three are really essential (and you can get two of them using texpand on your calculator). You can derive the rest from these three:
  - The trig form of the Pythagorean Theorem
  - Sine of a sum
  - Cosine of a sum
- Additional examples:
  1. #7, p. 500
  2. #27
  3. #42
  4. #56

Website maintained by Andy Long. Comments appreciated.