Day 15 in MAT229

Last time

Next time

Today:

Announcements:
- Homework 6.7 is due today; 6.8 is due Monday.
- Your test next week will be through 7.1.
- I've reserved computer lab 310 for tomorrow, Friday, 9/12, at 9:00. So those who are able may join me as we go over some of the basics of Mathematica. I've also reserved it for a couple of more Fridays, the 26th of September and the 3rd of October.
Let's finish up section 7.1: Integration by parts.
- First of all, the big picture: integration by parts is just the product rule backwards. This integration technique, like all integration techniques, is really just a differentiation technique in reverse.
  Consider the method of u-substitution, for example. That's just the chain rule in reverse.
- Derivation of the integration by parts formula:
  We start with the product rule:
  
  ${\left[u(x)v(x)\right]'=u(x)v'(x)+v(x)u'(x)}$
  Now integrate both sides:
  
  ${\int_{}^{}\left[u(x)v(x)\right]'dx=\int_{}^{}\left[{u(x)v'(x)+v(x)u'(x)}\right]dx}$
  
  ${\int_{}^{}u(x)v'(x)dx=u(x)v(x)-\int_{}^{}v(x)u'(x)dx}$
  
  ${\int_{}^{}udv=uv-\int_{}^{}vdu}$
- We'll motivate this technique by considering exercises #9 and #66, p. 492 in detail.
- Integration by parts may need to be carried out multiple times: sometimes the idea is to simplify the integral each time, until a really simple one arises allowing us to calculate the final solution (e.g. Example 6, p. 491). Sometimes it's something of a trick: we compute the integral multiple times in order to return to the original integral, allowing us to solve an equation for the original integral (e.g. Example 4, p. 490).
- Suggested strategy:
  - Choose u so that u' is simpler than u itself.
  - Choose v' so that $v=\int_{}^{}v'dx$ can be evaluated.
  - Sometimes v'=1 is a good choice.
- Of course, all this works with definite integrals:
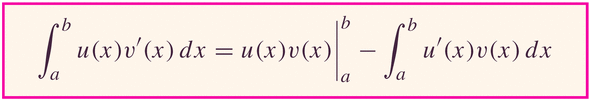
- Examples:
  1. #10, p. 492
  2. #39
  3. #40
  4. #41
  5. #42
  6. #52
section 7.2: Trigonometric Integrals
- We'll look at a few examples which illustrate the importance of trigonometric identities
  - #65, p. 501; this one prepares us for the two that follow.
  - #1
  - #6
- Now let's look at some of the useful identities that we'll want to use from time to time. The good news is that only three are really essential (and you can get two of them using texpand on a TI calculator, or TrigExpand in Mathematica). You can derive the rest of the trig identities from just these three:
  - The trig form of the Pythagorean Theorem:
    
    ${\sin^2(x) + \cos^2(x) ={1}}$
  - Sine of a sum
    
    ${\sin(A+B)=\sin(A)\cos(B)+\sin(B)\cos(A)}$
  - Cosine of a sum
    
    ${\cos(A+B)=\cos(A)\cos(B)-\sin(B)\sin(A)}$
- Additional examples:
  1. #7, p. 500
  2. #27
  3. #42
  4. #56

Links:

Integration by parts from an on-line textbook
Trig identities and their role in integration

Website maintained by Andy Long. Comments appreciated.