- Homework 6.8 is due today; 7.1 is due tomorrow.
- The first MAT 229 exam review will take place tonight, the 15th, from 4 pm to 6 pm in MEP 314.
- Your test this Thursday will be through 7.1. You may use a Scientific (but not graphing) calculator. You may not use a phone, or tablet, or any other type of calculator. So you've got three days to find a simple calculator!
- We'll look at a few examples which illustrate the importance of
trigonometric identities
- Now let's look at some of the useful identities that we'll want to
use from time to time. The good news is that only three are really
essential (and you can get two of them using texpand on a TI
calculator, or TrigExpand in Mathematica). You can derive the rest of
the trig identities from just these three:
- The trig form of the Pythagorean Theorem:
- Sine of a sum
- Cosine of a sum
- The trig form of the Pythagorean Theorem:
- Additional examples:
- #7, p. 500
- #27
- #42
- #56
- What's integration all about? Well, we usually start by going about calculating (signed) areas:
"dA" is called an "infinitesimal" -- it's a tiny chunk of area -- tinier than anything you know ("vanishingly small")!
What's numerical integration all about? We do pretty much the same thing, only we have
where the
are small, but not vanishingly small.
- There are various schemes for numerical integration:
- Left Rectangular
- Right Rectangular
- Midpoint
- Trapezoidal
- Simpson's rule.
- Three of the rules are so called "rectangle rules" (LRR, RRR, Midpoint Rule);
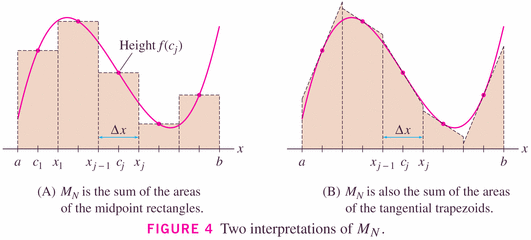
but as the image to the right (above) and the graphical insight below show, we can think of the Midpoint rule as being a "Tangent rule":
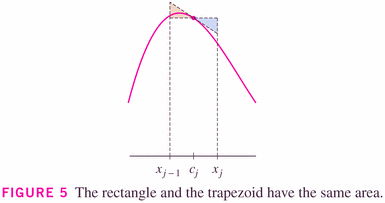

- The Trapezoidal rule is really just the average of the LRR and RRRs. This gives rise to an important observation, which I want to encourage you to think about, and here it is:
When you have two estimates, you have a third. (their arithmetic average, in this case).

- Simpson's rule is a "blend" (or weighted average) of the Midpoint
and Trapezoidal rules, which perfectly balances the errors of the two
to generate a better rule:
Notice that the number of subintervals in Simpson's rule must be even.
Now we can go further:
When you have two estimates, you have infinitely many more. (their weighted arithmetic averages).
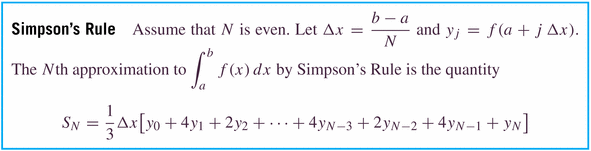


- Here is a hand out which emphasizes this message. Let's take a look at this:
- Check midpoint calculation
- Let's do the calculations by the formulas, for
- Trapezoid
- Simpson's
- Check that we get the same things using the averages
- Calculate the true value of the integral, and compare to the approximations. What's surprising?
- Examples:
- #29, p. 541
- Others?
- Links:
- Here's a nice summary of the issue, focused on the use of Mathematica to illustrate them. Interesting even if you don't use Mathematica.
- Numerical Integration on-line.
Website maintained by Andy Long. Comments appreciated.