- Homework 7.1 is due today; your next homework is due Monday (and another on Wednesday).
- Return of 6.8
- 4: Which are indeterminate?
- 12: Don't drop the limits....
- 100: This one wasn't as tricky as you thought.
- How did the exam review go?
- Your test this Thursday will be through 7.1. You may use a
Scientific (but not graphing) calculator. You may not use a phone, or
tablet, or any other type of calculator. So you've got three days to
find a simple calculator!
- Inverse functions:
- Obtaining inverse graphically from a given function f
- Obtaining function form from a given function f
- Relationship between domain and range
- "undoing" operation (identity function with f)
- Differentiation formula for inverses
- Exponential functions
- Two important types -- growing and dying. Know their graphs.
- Most important base: e (why e?)
- Changing bases
- Logs
- Inverse functions of exponentials. You know their graphs if you know the graphs of exponentials and can look in a mirror.
- Changing bases to ln
- Astonishing derivative of ln(x)
- Logarithmic differentiation -- a tool for differentiation some difficult characters
- Inverse Trig Functions
- Start with properties of trig functions -- e.g. parity (even/oddness)
- Definitions (trig functions aren't really invertible)
- Watch domain and range issues
- Graphical representations
- Derivatives (provide new antiderivatives for some useful functions)
- Hyperbolic trig functions
- Definitions
- Form of their graphs
- Properties and identities
- Their inverses (more antiderivatives)
- L'Hopital's rule
- A trick for evaluating some indeterminate limits.
- Turning indeterminate limits into quotients
- Integration by parts
- The product rule backwards.
- Identifying the product, and doing definite and indefinite integrals. (1 can be part of the product.)
- Other things you are expected to know (among others --
this list is not exhaustive, nor are those above)
- tangent lines
- limit definition of the derivative
- and other calc I things (e.g. u-substitution)
- Inverse functions:
- We'll look at a few examples which illustrate the importance of
trigonometric identities
- Now let's look at some of the useful identities that we'll want to
use from time to time. The good news is that only three are really
essential (and you can get two of them using texpand on a TI
calculator, or TrigExpand in Mathematica). You can derive the rest of
the trig identities from just these three:
- The trig form of the Pythagorean Theorem:
- Sine of a sum
- Cosine of a sum
- The trig form of the Pythagorean Theorem:
- Additional examples:
- #7, p. 500
- #27
- #46
- #56
- What's integration all about? Well, we usually start by going about calculating (signed) areas:
"dA" is called an "infinitesimal" -- it's a tiny chunk of area -- tinier than anything you know ("vanishingly small")!
What's numerical integration all about? We do pretty much the same thing, only we have
where the
are small, but not vanishingly small.
- There are various schemes for numerical integration:
- Left Rectangular
- Right Rectangular
- Midpoint
- Trapezoidal
- Simpson's rule.
- Three of the rules are so called "rectangle rules" (LRR, RRR, Midpoint Rule);
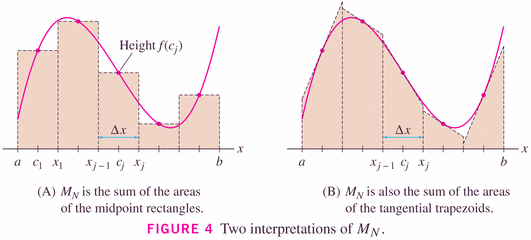
but as the image to the right (above) and the graphical insight below show, we can think of the Midpoint rule as being a "Tangent rule":
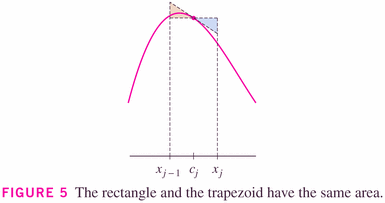
Be careful however not to confuse the midpoint and trapezoidal rule. The trapezoid represented above is not the same as the trapezoid of the trapezoidal rule.

- The Trapezoidal rule is really just the average of the LRR and RRRs. This gives rise to an important observation, which I want to encourage you to think about, and here it is:
When you have two estimates, you have a third. (their arithmetic average, in this case).

- Simpson's rule is a "blend" (or weighted average) of the Midpoint
and Trapezoidal rules, which perfectly balances the errors of the two
to generate a better rule:
Notice that the number of subintervals in Simpson's rule must be even.
Now we can go further:
When you have two estimates, you have infinitely many more. (their weighted arithmetic averages).
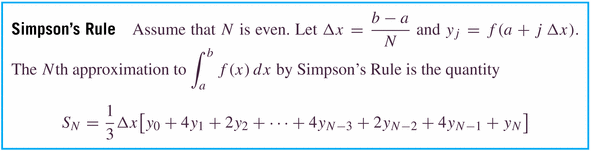
Here are the error bounds, that illustrate that the errors of midpoint and trapezoidal are related, and suggest how to combine them to create a better method (Simpson's rule):


- Here is a hand out which emphasizes this message. Let's take a look at this:
- Check midpoint calculation
- Let's do the calculations by the formulas, for
- Trapezoid
- Simpson's
- Check that we get the same things using the averages
- Calculate the true value of the integral, and compare to the approximations. What's surprising?
- Examples:
- #29, p. 541
- Others?
- Links:
- Here's a nice summary of the issue, focused on the use of Mathematica to illustrate them. Interesting even if you don't use Mathematica.
- Numerical Integration on-line.
Website maintained by Andy Long. Comments appreciated.