- Your 11.8 homework is returned:
- 14
- 16
- 38
- Your 11.9 homework is due.
- You have an exam on Tuesday. It will cover 11.2 through 11.9.
- We'll have a review on Monday, and I'll be here tomorrow at 9:00, for anyone who wants to come in for some extra practice.
- Sorry, but last time I forgot to mention Lauren's review last night: did anyone go?
- The big picture: we're approximating functions (some nasty) with nice ones (polynomials):
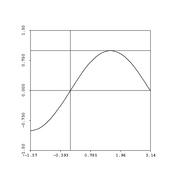
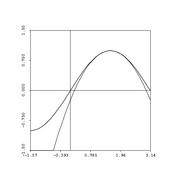
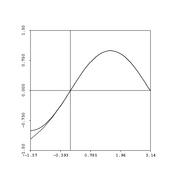
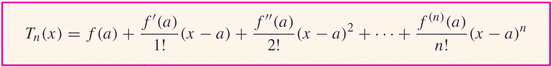
Let's talk error now. Remember error? As we discussed for the case of Simpson's rule, it's nice to give an estimate -- but even nicer when you can provide an error estimate, also....
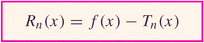
Now, provided
goes to zero as
on the interval
, the function
is equal to its https://www.youtube.com/watch?v=e4MSN6IImpI Taylor series on
.
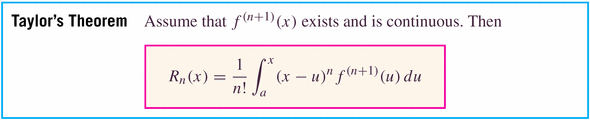
There are actually various forms of the remainder term. This one is kind of nice, because we can see how to obtain the following bound:
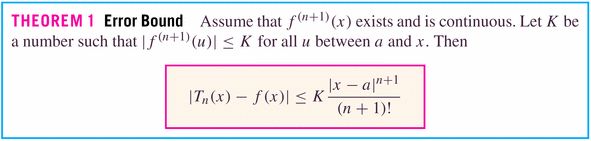
- Examples:
- Let's find the Taylor series for ln (which is one that Nick asked about) around 3. That is, we're looking for values of
for arguments of around
. We can do it in two different ways:
- using our favorite geometric series, and
; or
- using Taylor polynomials, and
.
- using our favorite geometric series, and
- Taylor Polynomials Lab (from Stewart's Calculus)
This exercise (and Taylor series in general) emphasizes that the behavior of a function may be completely dictated by the derivatives of the function at a single value of x=a:
Local behavior determines global behavior, but we need an infinite amount of local information (all derivatives evaluated at x=a).
This is an astonishing observation.
For this exercise we're approximating f(x) in the vicinity of x=a, however, by using only a finite amount of derivative information at x=a. Hence there will be errors.
I've added a few "supplementary" elements to my solution, such as the error in the 8th Taylor polynomial as well as the error bound:
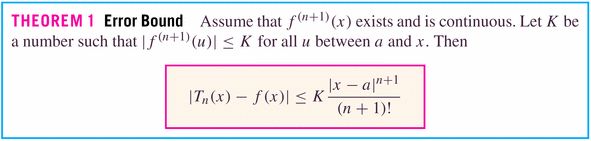
- Let's find the Taylor series for ln (which is one that Nick asked about) around 3. That is, we're looking for values of
- This section is about applications of Taylor series, which
is something that I've been emphasizing from the beginning. You should
read the section, but there aren't a whole lot of "new" techniques
described in the section. It's more about showing how Taylor series
are used (which is very important, of course).
Emphasis is on the following:
- Error estimation: we're going to make mistakes, but how bad will they be? Or can we get the errors under whatever limbo bar has been established? This is often in the context of evaluating a function at a point.
- A sensible use of a simplified version (Taylor polynomial) of a function in some important domain (where the function itself is "overly complicated"). This is often in the context of replacing a function in a special domain.
- So we'll do a
few applications from the problems, to illustrate
some of the power of Taylor series:
- #18
- #19
- (By the way: you don't always have to calculate derivatives, if you can do it in an easier way... That goes for both #18 and 19 above)
- #32