- Reminder: turn off your rectangles!
- You have an assignment to turn in for next time....
You're certain that this object must have some very interesting mathematical content, but aren't sure what. But you'd certainly like to know!
Last time we made a few conjectures, which are guesses that we seek to confirm or deny. Some were relatively straightforward, others more complicated:
- That single bars represented 1
- That we add up individual bars to get higher numbers: 2, 3, etc. -- but that things seem to fail at some point (6). We're seeing some patterns, and then they fail -- or rather, we didn't completely get the pattern.
- Someone speculated that each row of the triangle can be obtained from the previous row, by addition (somehow).
- Someone else speculated that if you add up each successive row, you get twice the previous row.
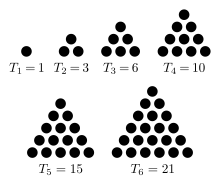
I asked you to fill in the triangle, using our numbers. It's most convenient to do so using the hexagonal grid on the other side of your sheet. Let's do that now.
How do we understand this triangle? What kinds of numbers do we see? One kind is suggested by that last conjecture, above, and we'll be talking more about those today.
Let's take a look at a few more features of this triangle, which is commonly called Pascal's triangle:
- Different kinds of numbers appear in diagonals, which we should all be able to identify:
- a line of 1s
- the counting numbers
- triangular numbers
- tetrahedral numbers:
- Diagonals can be thought of as "accumulators"
Counting is a critical step in probability, and the Pascal in "Pascal's Triangle" is Blaise Pascal (1623-1662), who studied it to help him compute probabilities:
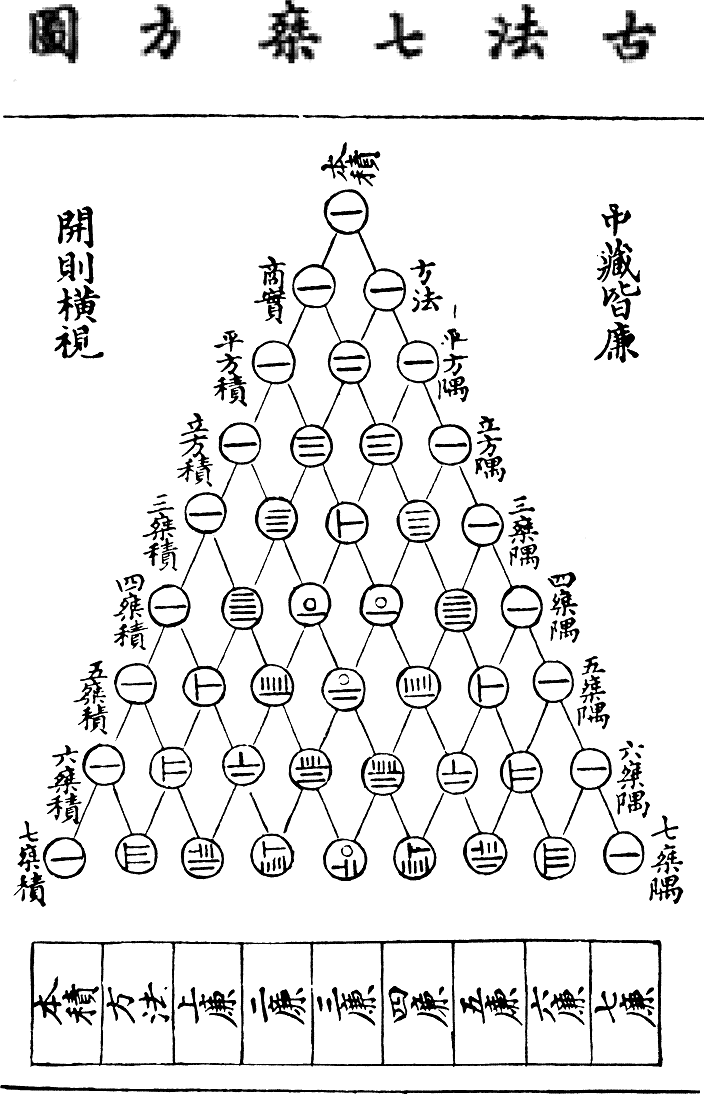
The triangle was known long before Pascal, however: on one side of your handout is the 13th century Chinese version of our triangle; but that's not the oldest known version.
Interestingly enough, there's a mistake in one row of the Chinese version of this table. Can you find it?
One thing that Pascal's triangle allows us to do: it allows us to understand how this Chinese culture of the 13th century wrote its numbers (Chinese Bamboo Counting Rods). How did these people write 15? 28? 30?
I asked you to do the reading "From Fish to Infinity" for today, in which we learn the answer to one of life's persistent questions:
We learn something of that, anyway -- at least about six fish. But
We learn that
- "...numbers are shortcuts for counting by ones...." (p. 5)
- Furthermore, "...Humphrey might realize he can keep counting forever." (p. 5) -- something that will be very important when we come to talk about infinity.
Did you notice Humphrey using any other cues to help him keep track of the number of fish?
- How does the game work?
- Can you win at the game? You should be able to do it every time!
- Here's the handout for the cards, if you want to print off another copy.
- Each of you will be part of a team of three, taking turns playing the roles of contestant, Fraudini, and someone to check the play.
So the key can be found in Pascal's triangle! It seems that just about everything can be found there....