Day 3, MAT115

• Announcements:
  • Reminder: turn off your rectangles!
  • Please turn in your first assignment.
  Question of the day: How do we count without counting?

• Last time we learned a little more about
  

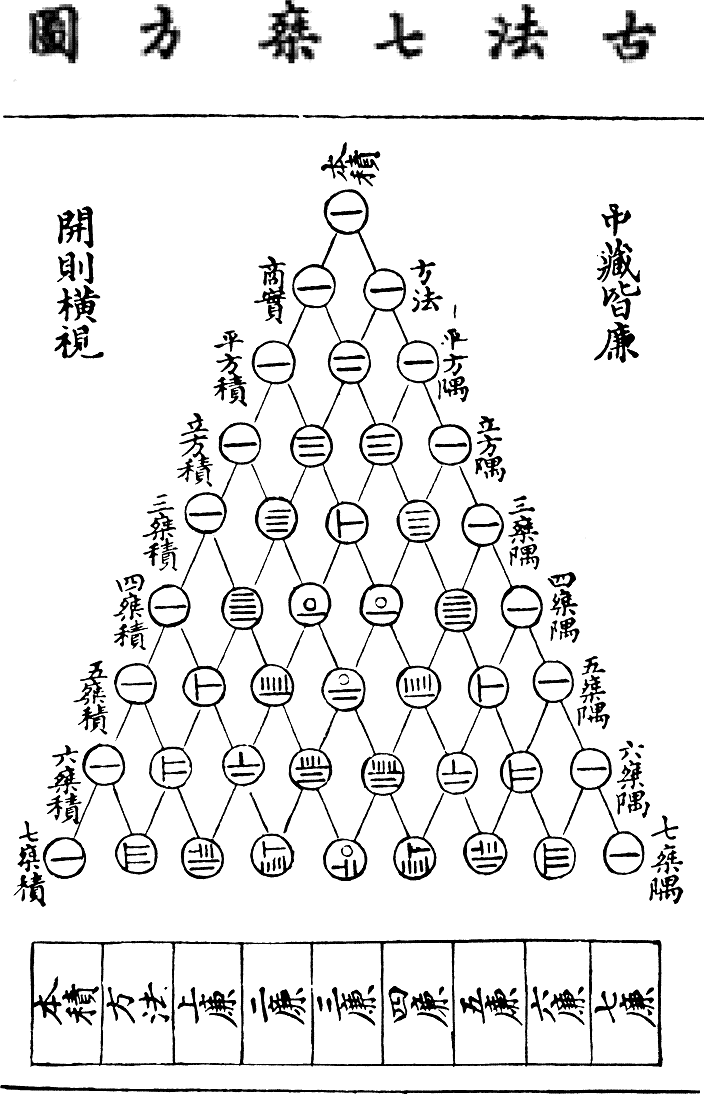
  (aka Pascal's triangle).

  You should be able to recreate Pascal's triangle, and know what numbers are contained therein.

  We were also paid a visit by The Great Fraudini, who used powers of 2 (which are found in Pascal's triangle as the sums of the rows) to "read peoples' minds!" I hope that you made a buck or two reading minds this past weekend....

  What questions do you have about either Pascal's triangle or about The Great Fraudini's trick? The secret of Fraudini's trick is this:

  Every counting number is either a power of 2, or can be written as a sum of distinct powers of 2 in exactly one way.

• Today we want to discover another use of powers of 2; an ancient use. We also want to check in with our author, on "Rock Groups".

• Let's dive into today's first new topic: How might "primitive" people have counted? (We'll use a mathematical concept called a "tree" (a type of graph) to help us. More on those later....)

  There are at least three good suggestions that I know of:

  • Tallies (your next assigned reading talks more about tallies).

  • One-to-one correspondence
    • using body parts -- "one hand" of sheep, say -- meaning five sheep.
    • cairns

  • And then an unusual method of "counting by partitions" that Patricia Baggett and Andrzej Ehrenfeucht proposed at the 2011 National Math Meetings.
    • Let's begin by counting some students their way....

    • They proposed that primitive societies may have counted this way. Let's suppose you need to let the King know how many sheep you have:
      1. divide your sheep equally ("one for you, one for me") into two pens: either there is one left over, or not. You make a note of whether there is one left over or not.
      2. Send all the sheep in pen two (and any "left over") out to pasture, and then
      3. You divide the sheep in pen one into pens one and two: i.e., just do it again! And again, and again, and.... until you get down to a pen one with just sheep in it.
      4. Now let's see how we might record the results to send to the King.

         The easiest way to illustrate the counting method is via a tree.

         Let's see how we might use a tree to represent the solution to the "22" counting problem: in the linked example, we would get 10110 by writing the remainders from left-to-right starting from the bottom of the tree. (The result should always start with a 1 if done correctly, since we always end with one sheep!)

         

         The answer will be written as 1, 0, 1, 1, 0

         That is, from the bottom up, left to right. This is important! We have to have a consistent scheme for writing.

         So how do we write

         • 9 sheep
         • 31 sheep
         • 54 sheep

      5. Can you go backwards? How many sheep is meant by
         1. 1,1,0,1,1,0,0
         2. 1,1,0,1,1,0,0
         3. 1,0,0,1,0,1,1,0,1

         Try making a tree with these remainders.

      6. and now let's count some coins:
         1. We'll be counting pennies - in small groups.
         2. Divide your penny rolls up (no need to do it evenly!)
         3. Get your answer, then check answers with another nearby group.
         4. Compare (and record) your answers

• Let's continue by considering Chapter 2 from our text: rock groups. To explore, we'll use pennies (rather than rocks), and you'll work with a partner.

  We want to understand each of these notions:

  • prime,
  • composite,
  • square, and
  • triangular numbers
  but understand them as concrete things, as objects (e.g. pennies).

  So we're interested in arranging our pennies (i.e. rocks) in groups with certain properties.

  All numbers of pennies can be arranged into a line (this is Humphrey's "Furry Arms" method):

  

  Some numbers of pennies can be arranged into

  • rectangles (of more than one row):
    

    Note that this is how Humphrey said the number of fish -- he blocked the fish into two groups of three fish --

    fish fish fish,
    fish fish fish
  • squares
  • triangles

• If a number greater than one can be expressed as a rectangle of more than one row, then it is composite; otherwise, it is prime. The rows must stack to form a rectangle, which means that they can be put in one-to-one correspondence with each other (see the picture above).

  Another way of saying that a number is composite is to say that it can be broken up into groups (each with more than one member) that can each be put into one-to-one correspondence with each other (that is, each element in one group has a partner in another -- and just one partner. Perfect for the dance....).

  So 9 is an example, a square. It can be broken into three groups of three; so each group of three can be put into one-to-one correspondence with any other group of three.

  Notice that we said greater than one in the definition above. The number 1 is special, and considered neither prime nor composite.

  We've already heard this important rule, which you learned at some point in your mathematical education:

  Every natural number (other than 1) is either prime, or can be expressed as a product of primes in a unique way.

  Let's look at examples of each.

  1. Using your pennies, make (and document) all rectangles for pennies up to 15. Then answer me this: "What's special about 12?"
  2. Find and illustrate the triangular numbers until you run out of pennies!

• There is an interesting observation made by the author. It was about odds and evens. What do Strogatz notice about the sum of
  • odd and even
  • odd and odd
  • even and even
  Let's make a table to illustrate that:

  +	Odd	Even
  Odd
  Even

  Rock groups suggest formulas for representing even and odd numbers:

  Evens:	2*n
  Odds:	2*n+1

• How do we say the formula suggested at the top of page 10? (By the way, add one more row to the top of the equations near the top of the page - what would the row be?

  How would you say what's happening in words? What do you think of the proof of the "theorem" at the bottom of the page?

  1. Do you see the theorem expressed in the rocks?
  2. Can you see the form "2n+1" in the rocks?
  3. I see a new theorem: T₅+T₄=5² (In words, "the sum of the fourth and fifth triangular numbers is the fifth square".) By playing with rocks we discover relationships. It's probably how primitive civilizations did it, too!

• The story of the "The Housekeeper and the Professor" is interesting, and modelled on a famous mathematical event -- the story of child prodigy Carl Friedrich Gauss:
  

  Once again, rock groups give us a formula for representing triangular numbers. So let's go through the reasoning for the housekeeper's answer.

fish fish fish
fish fish fish