- Sarah's talk was great. Good work Sarah!
- Homework for 16.2 is due.
- Your 16.1 homework is returned:
- #5: vectors are all unit vectors
- #26: vectors are again all unit vectors, and should point away from the origin.
- #20: I didn't grade this one, but I saw some plots that
told me that I should say something:
the vectors are all pointing towards or away from the origin, because they're proportional to the position vector.
- We looked at #36 in class already....
- Quizzes are returned. There were three ways (at least) to do this quiz:
- Symmetry (and one known function) alone. You do it.
- Using properties of functions alone
- Computing gradients and using the two ideas above.
- I still haven't finished your exams....:(
- Parameterizing images
- Last time I tried to motivate path independence, which follows
from the fundamental theorem (the we reflected back on #8,
p. 1096, which was far easier to do using the fundamental
theorem).
In this section there are certain definitions that we want to make note of:
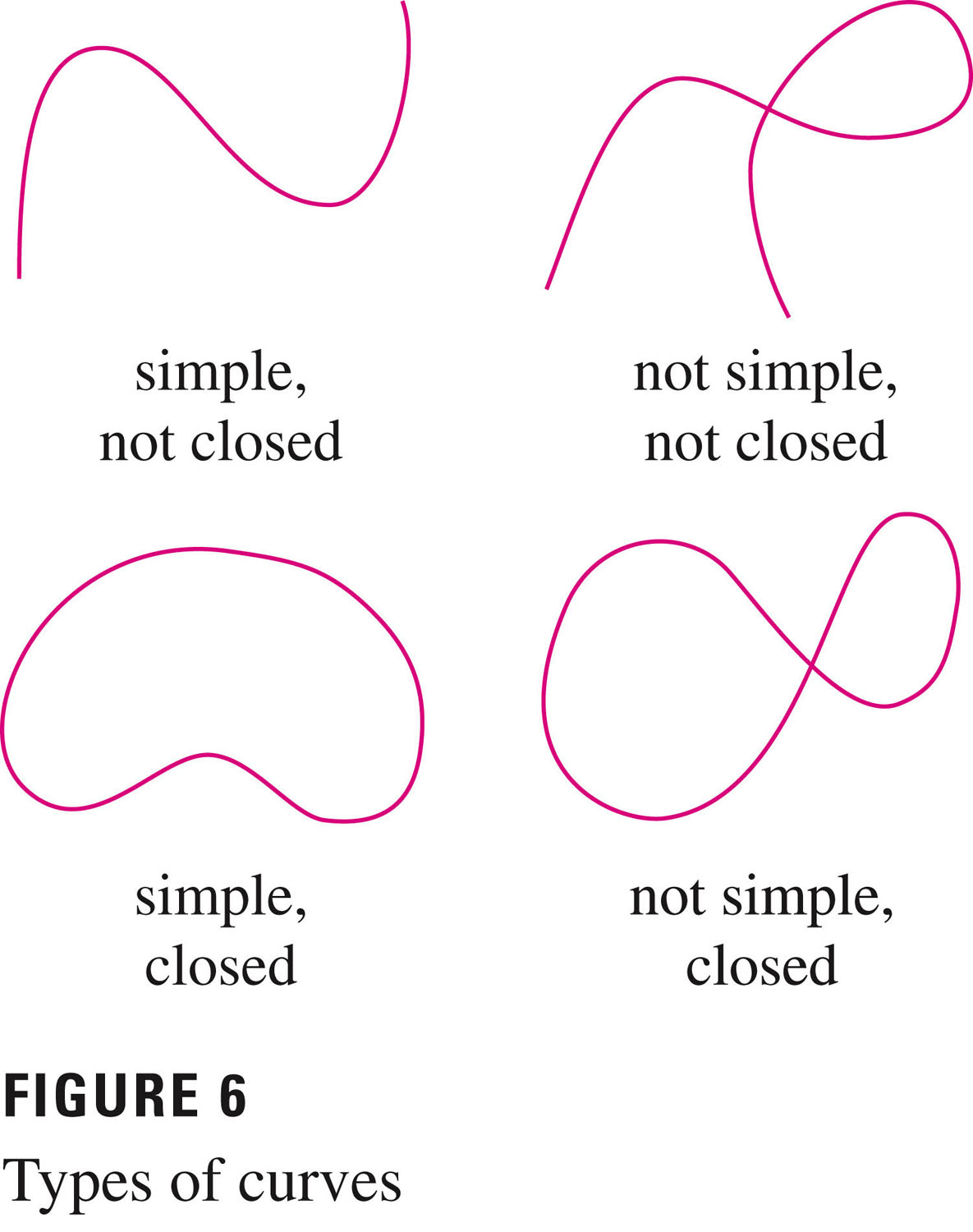
Let $C$ be a smooth curve (note -- smooth!) given by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Let $f$ be a differentiable function of two or three variables whose gradient vector $\nabla f$ is continuous on $C$. Then \[ \int_{C} \nabla f \cdot d{\bf{r}} = f({\bf{r}}(b)) - f({\bf{r}}(a)) \]
As the author mentions right after his proof, this is also true for piecewise smooth curves.
Examples:
- #1, p. 1106
- #3
- By hook, or
- By crook:
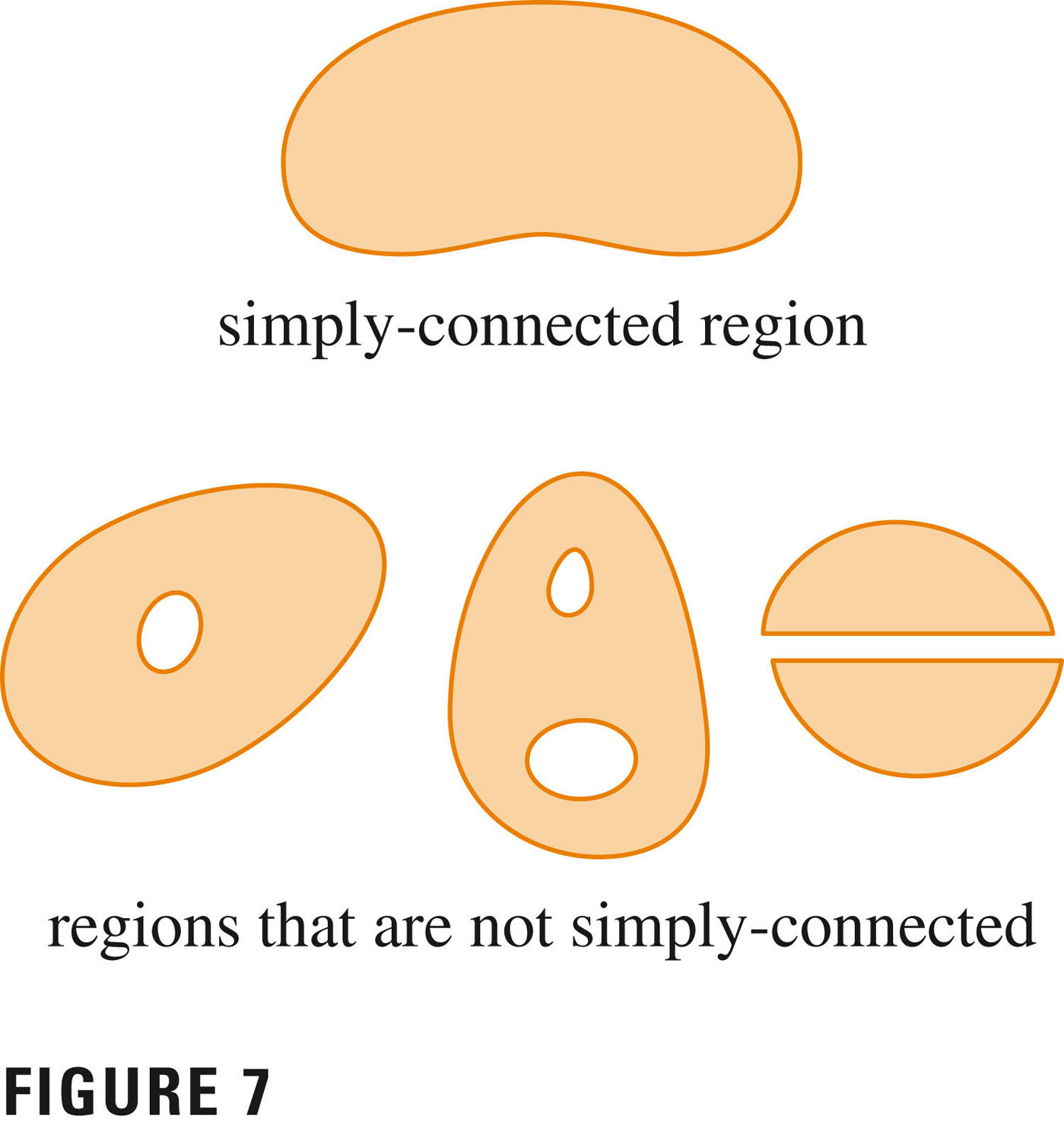
Let ${\bf{F}} = P {\bf{i}} + Q {\bf{j}}$ be a vector field in an open, simply-connected region $D$. Suppose that $P$ and $Q$ have continuous first-order derivatives and \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \hspace{1in} \ throughout\ D \] Then ${\bf{F}}$ is conservative.
- Now let's have a look at the very important problem of the conservation of
energy, p. 1105.
- Let's see why the "crook" works above. We'll do it via theorem 5,
p. 1102:
If ${\bf{F}}(x,y) = P(x,y) {\bf{i}} + Q(x,y) {\bf{j}}$ is a conservative vector field, where $P$ and $Q$ have continuous first-order partial derivatives on a domain $D$, then throughout $D$ we have \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \] This says that mixed partials of $f$ (essentially the potential of $ \bf{F}$) are equal -- the proof is Clairaut's theorem! $P=f_x$ and $Q=f_y$, and their partials are continuous (so the second partials of $f$ are continuous), so, by Clairaut's theorem, \[ f_{xy}=\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}=f_{yx} \]
- There are a couple of theorems that inform us about path
independence, which we want to at least state. We've talked about
path independence enough that you might be able to guess these by now:
- The definition:
\[
\int_{C} {\bf{F}} \cdot d{\bf{r}}
\]
is independent of path if
\[
\int_{C_1} {\bf{F}} \cdot d{\bf{r}} = \int_{C_2} {\bf{F}} \cdot d{\bf{r}}
\]
for any two paths $C_1$ and $C_2$ in $D$ that have the same initial and
terminal points.
- Theorem: Suppose ${\bf{F}}$ is a vector field that is continuous
on an open connected region $D$. If $\int_{C} {\bf{F}} \cdot d{\bf{r}}$
is independent of path in $D$, then ${\bf{F}}$ is a conservative vector
field on $D$; that is, there exists a function $f$ such that $\nabla f
= {\bf{F}}$.
- The fundamental theorem tells us the converse of that: if ${\bf{F}}$ is a gradient (conservative) vector field continuous on an open connected region $D$, then it's path independent.
- #11, p. 1106
- #21
- #35 -- assumptions matter! What's the domain of ${\bf{F}}$?
- The definition:
\[
\int_{C} {\bf{F}} \cdot d{\bf{r}}
\]
is independent of path if
\[
\int_{C_1} {\bf{F}} \cdot d{\bf{r}} = \int_{C_2} {\bf{F}} \cdot d{\bf{r}}
\]
for any two paths $C_1$ and $C_2$ in $D$ that have the same initial and
terminal points.