- Your exam redos are due today. Remember, you can turn them in at
Sarah's KAS talk tomorrow (but you must attend the talk as well -- no
turning in for someone else).
- Sarah Stryffeler is giving a talk on Saturday, Nov. 14 at 2:15 in
GH 201. It concerns her work on measuring greenhouse gases. She will
also have a poster for OVSOT on Friday the 13th, and will be in the SU
ballroom presenting before class and after two.
Stop by and support her!
Anyone more news Jamie?
- The line integral of $f$ along $C$ is
\[
\int_{C} f(x,y)ds = \lim_{n \to \infty}\sum_{i=1}^{n}f(x_i^*,y_i^*)
\Delta s
\]
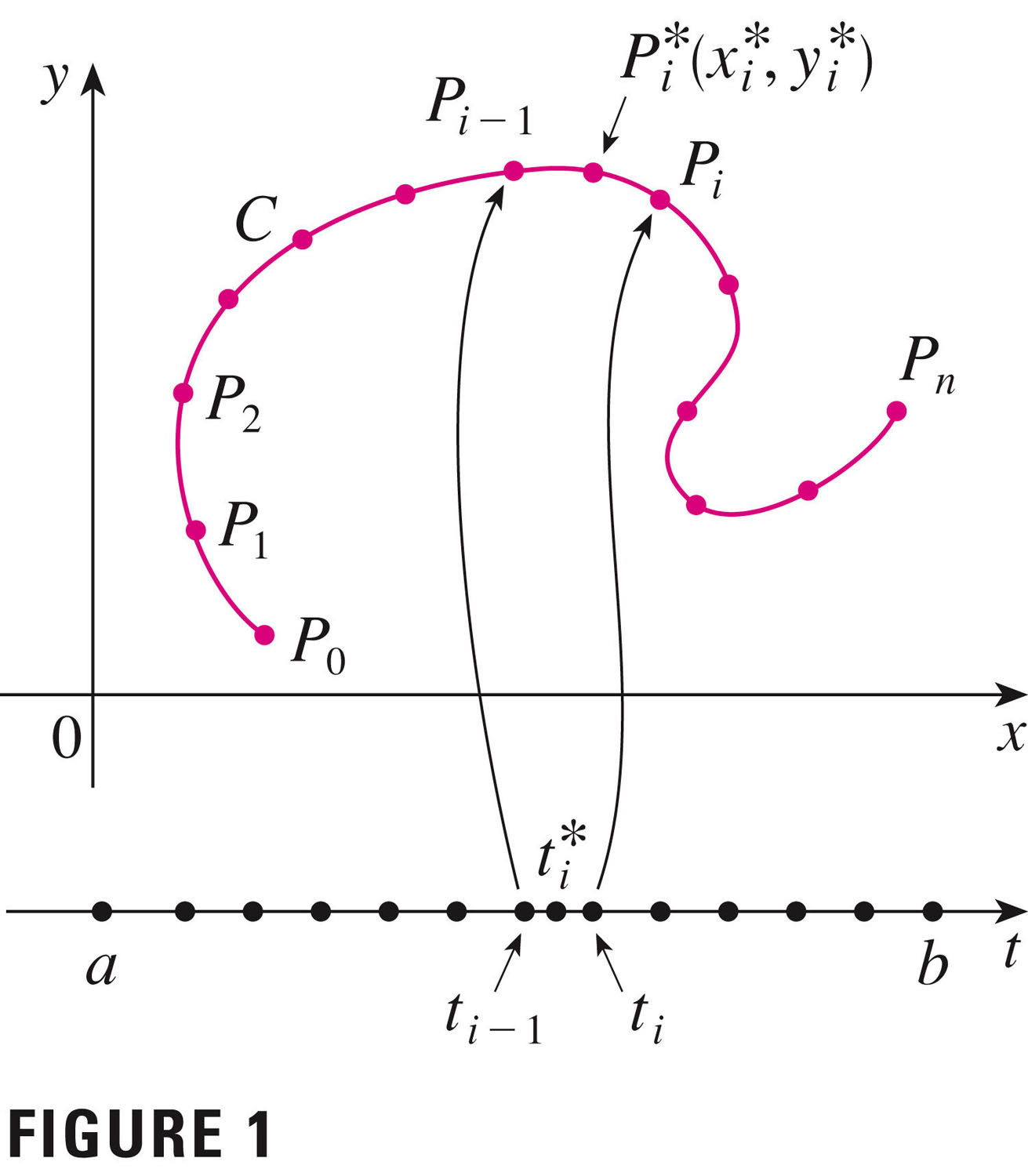
- If $f$ is continuous, then
\[
\int_{C} f(x,y)ds = \int_{a}^{b} f(x(t),y(t))
{\sqrt{\left(\frac{dx}{dt} \right)^2 +
\left(\frac{dy}{dt} \right)^2
}}
dt
\]
and this is independent of the parameterization $(x(t),y(t))$ (provided
the curve is traversed just once) as $t$ increases from $a$ to
$b$.
We can think of this as an area, per Figure 2 (if $f$ is positive):
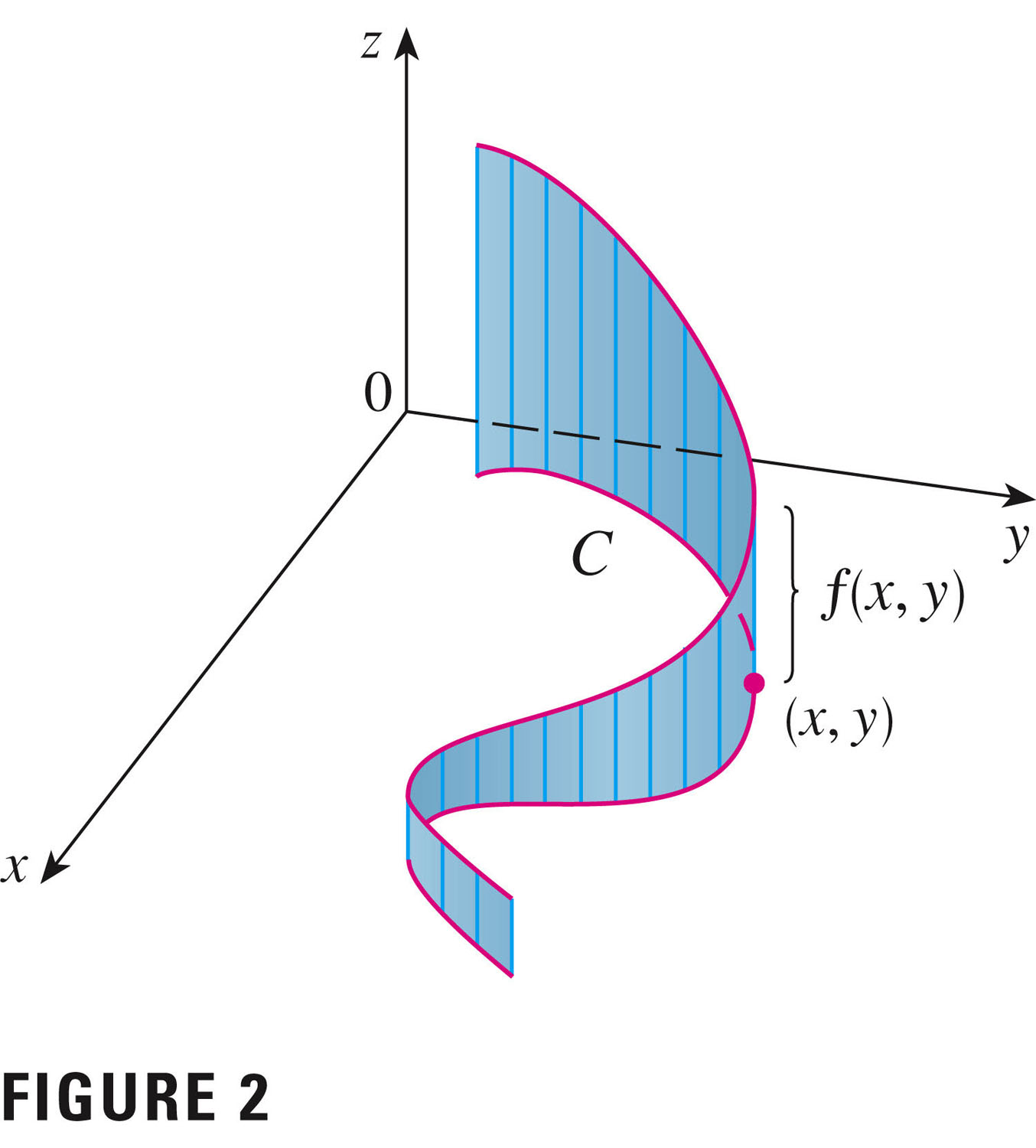
Although with $f(x,y)=1$ we can also think of this as the length of the curve. Note: we think of $dt$ as positive (and it is, because we've specified the orientation). But if we reverse the orientation, we'd need to "reverse $dt$" as well.
- Rather than look at line integrals along the curve $C$, with differential $ds$, we could integrate components along the $x$ and $y$ directions: line integrals of $f$ along $C$ with respect to $x$ and $y$ are \[ \int_{C} f(x,y)dx = \int_{a}^{b} f(x(t),y(t)) x^{'}(t) dt \] and \[ \int_{C} f(x,y)dy = \int_{a}^{b} f(x(t),y(t)) y^{'}(t) dt \]
- Let's look at Example 4 first, then take on #8, p. 1096.
Example 4, p. 1091,
- raises the issue of orientation;
- illustrates two different strategies of parameterization;
- telegraphs a topic of section 16.3: path independence of line integrals.
- We can think of re-think this one as a vector field problem.
- Examples:
- #8, p. 1096 (with lots of extra detail)
- #12 (3-d versions of all of this is no big deal)
- Now we want to extend our line integrals to vector fields.
First of all, let's get oriented: instead of thinking of the position as given by a point, we'll indicate it by a position vector, with starts at the origin and has its tip at the point of interest:
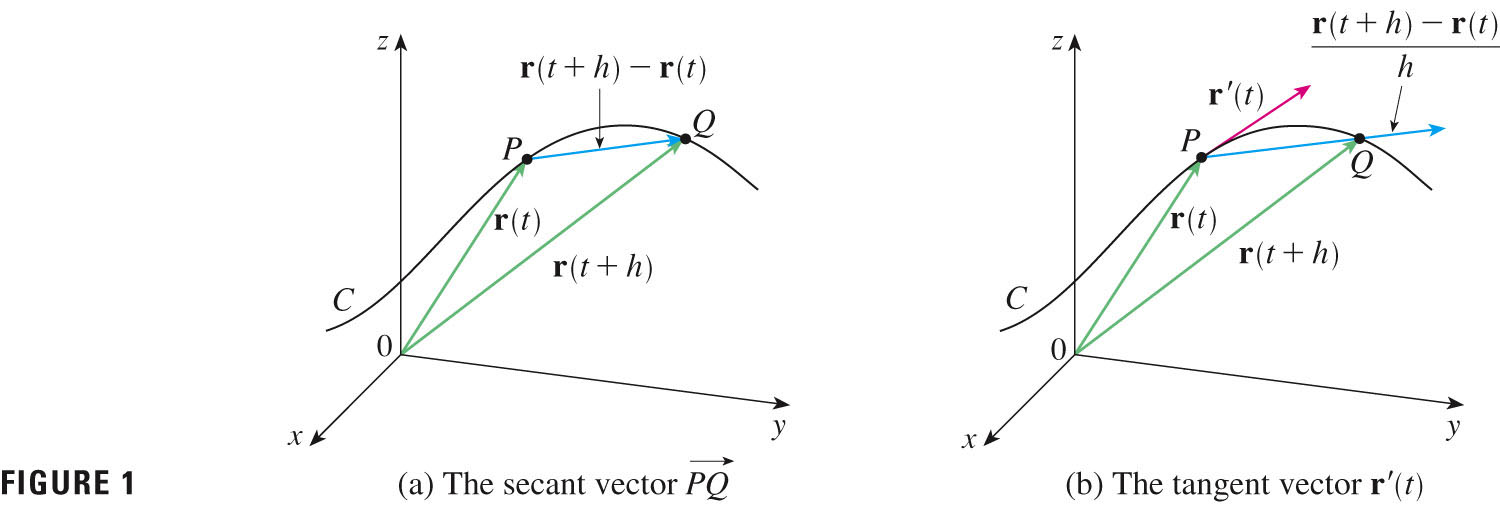
Then $d{\bf{r}}=\langle dx,dy,dz\rangle$, in particular.
Let ${\bf{F}}$ be a continuous vector field defined on a smooth curve $C$ traced out by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Then the line integral of ${\bf{F}}$ along $C$ is \[ \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot d{\bf{r}} = \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot {\bf{r}}^{'}(t) dt \]
If vector field ${\bf{F}}=P\hat{i}+Q\hat{j}+R\hat{k}$=$\langle P,Q,R \rangle$, then we can break the integral into three: \[ \int_{C} {\bf{F}} \cdot d{\bf{r}} = \int_{C} Pdx + Qdy + Rdz \] since $d{\bf{r}}=\langle dx,dy,dz\rangle$. With my parentheses fascination, you can be sure that I'd like to put parentheses around that last integrand: $\int_{C} (Pdx + Qdy + Rdz)$ -- just to emphasize that the integration is over all....
- #32, p. 1097
- #52
- First I want to motivate path independence, with the fundamental theorem.
- Then we'll consider the very important problem of the conservation of energy, p. 1105.
- Finally we'll reflect back on #8, p. 1096.